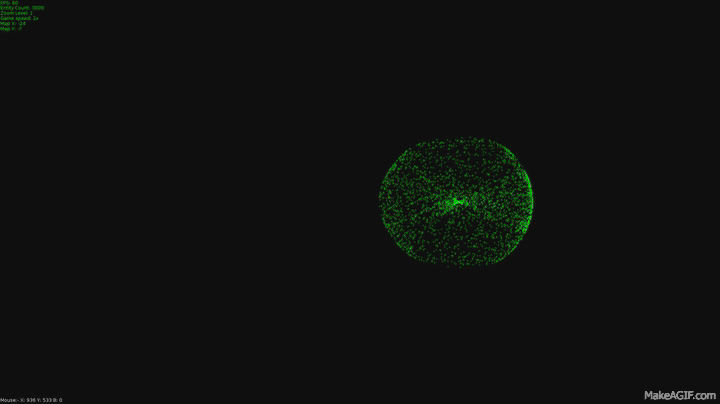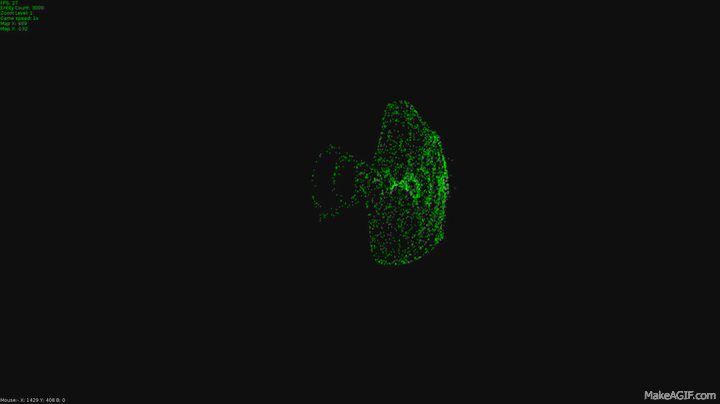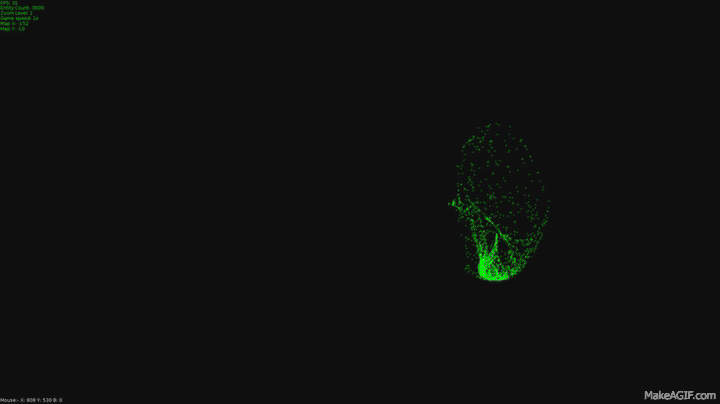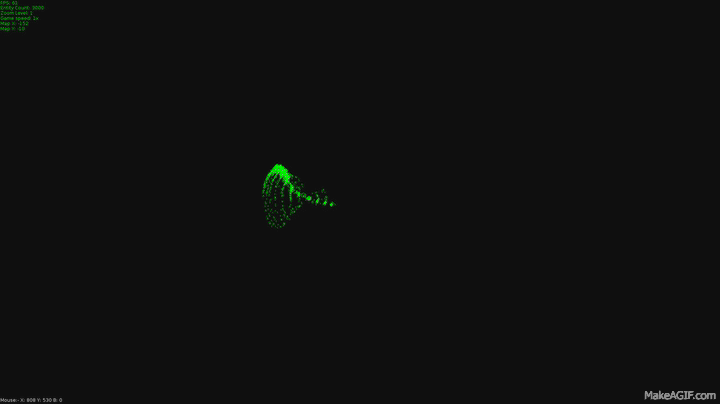
Studying Pythagoras may seem a bit dull at school but this 1800 year old subject is actually the mathematics of movement.
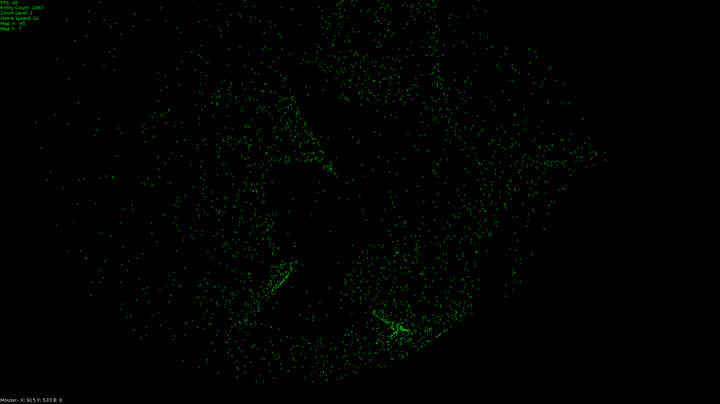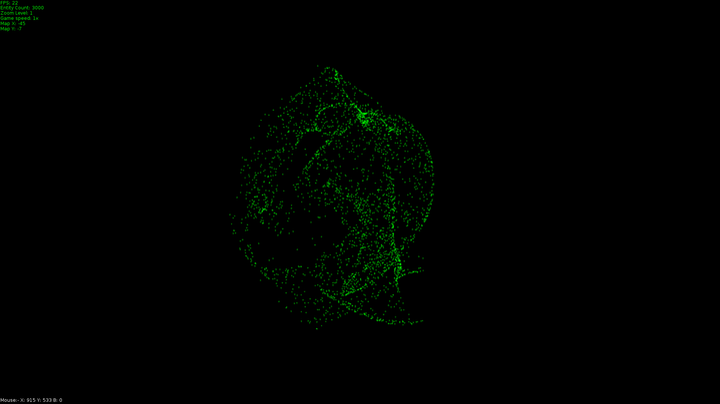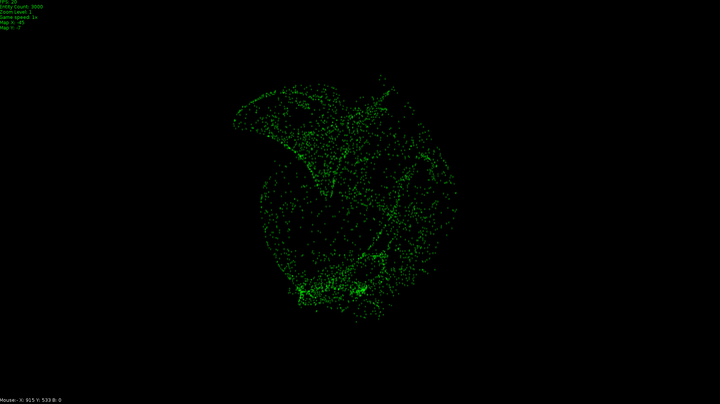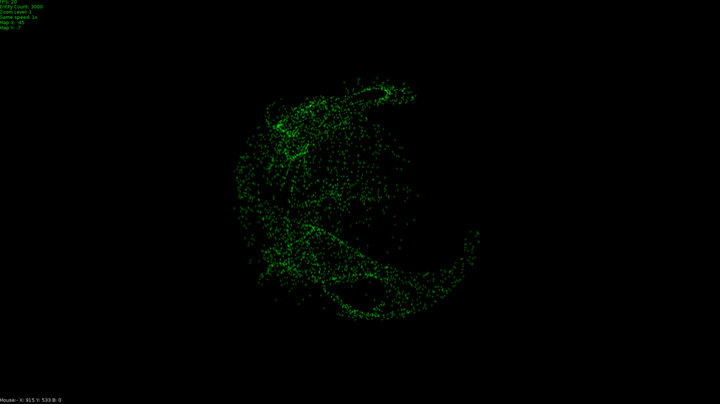
These were made by a program I wrote to simulate flocking and swarming, I wrote it as a test for fighter ship behavior for a game I'm making but thought they might be pretty enough to get you interested in the mathematics used to make them.
An Introduction to Vectors.
A vector is just a collection of numbers, I'll be using 2D vectors to explain but vectors come in all manner of dimensions. Vectors in 2D look like this,
a = {x = 10, y = 10}So here's our new vector a, it has 2 parts inside, an x value and a y value. Not much on it's own but it is exactly the right amount of information to describe a point in 2D space. Let's make a new vector, this time we'll call it b.
b = {x = 14, y = 13}With 2 vectors things get a little more interesting, let's pretend that a is our current location and while we're pretending we'll make b our destination. Then let's go totally wild and make believe that we're talking about Kilometers as units.
How far is a from b? Well to answer that we'll need to use some subtraction.
Vector Subtraction, A.K.A. Regular Subtraction.
Subtracting a from b is very simple, you take away a.x from b.x then take a.y from b.y, let's put that data into a new vector we'll call it d for difference.
d = b - a ord = {x = (b.x - a.x), y = (b.y - a.y)} ord = {x = 4, y = 3}Now we have a new vector d but this one doesn't describe a point, this one describes a direction instead. This is where it gets interesting, d.x and d.y are two sides of a right angle triangle so calculating the distance between a and b is simple Pythagoras.
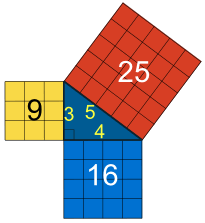
The hypotenuse of this triangle is 5 so our answer is b is 5 Kilometers away. We call the hypotenuse of this right angle triangle the magnitude of our vector, this line points to our destination, but how do we get there?
Let's talk Velocity.
Velocity put simply is our current direction of travel. As it's a direction we can also express it as a vector, let's be imaginative and call this one v.
v = {x = 0, y = 0}Those of you that are eagle eyed will have noticed already that we have a problem, if v.x and v.y are both zero then we aren't going anywhere. We'll need to apply some force.

Acceleration is the rate at which we can change our velocity, we'll need another new vector to show our acceleration which we can add to our velocity, we'll call it f but how do we calculate f? First we need one more piece of information, our maximum rate of acceleration. Let's say just for the sake of argument that this is half a kilometer an hour, now that we know our rate of acceleration we can start calculating f.
Vector Division A.K.A Regular Division.
We know which direction we need to go already but the magnitude of d is too big, 5 is much higher than 0.5 so first we'll need to normalize our direction vector. This sounds harder than it is, to normalize a vector all we need to do is divide the x and y components by the magnitude. In our case:
4 ÷ 5 = 0.8 3 ÷ 5 = 0.6Now we've normalized our force vector let's calculate the new magnitude, we could use Pythagoras again but this time we can use a little trick. Because we have divided d.x and d.y by 5 then we can just divide the magnitude of d by 5, 5 divided by 5 is 1. That's what normalizing does, it reduces the length of any vector to 1 which we can then multiply by our acceleration speed to figure out how fast we need to go. Let's plug those numbers into our force vector.
f = {x = 0.8 x 0.5, y = 0.6 x 0.5} orf = {x = 0.4, y = 0.3}Now that we have a location, a destination, a velocity and an acceleration force we can start to do a little basic physics.
Let's get Physical. ;)
Calculating movement over time is really quite simple, acceleration is added to our velocity, our velocity is added to our location and our acceleration gets reset to zero as we're no longer adding any new force now we're moving. Adding two vectors together is just like subtracting two vectors, we take the two x values and add them then take the two y values and add them. Let's look at our vectors after one hour.
v = {x = 0.4, y = 0.3}a = {x = 10.4, y = 10.3}do this a few more times and we'll be at b in no time! I'll write out our position at all the time points here so you know there's no cheating.
a = {x = 10.8, y = 10.6}a = {x = 11.2, y = 10.9}a = {x = 11.6, y = 11.2}a = {x = 12.0, y = 11.5}a = {x = 12.4, y = 11.8}a = {x = 12.8, y = 12.1}a = {x = 13.2, y = 12.4}a = {x = 13.6, y = 12.7}a = {x = 14.0, y = 13.0}That's the basics of getting from a to b, this is a very simple example as there are no other forces acting on us and I didn't even cover braking but I hope now that you can see that any other force, for example braking or friction, would just be another vector that we can add to our velocity to modify the results.
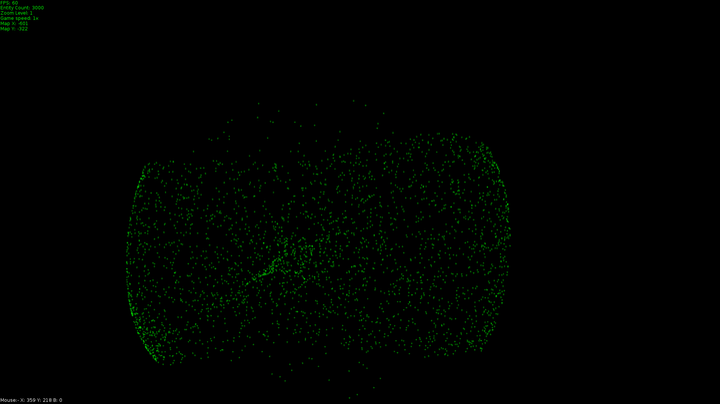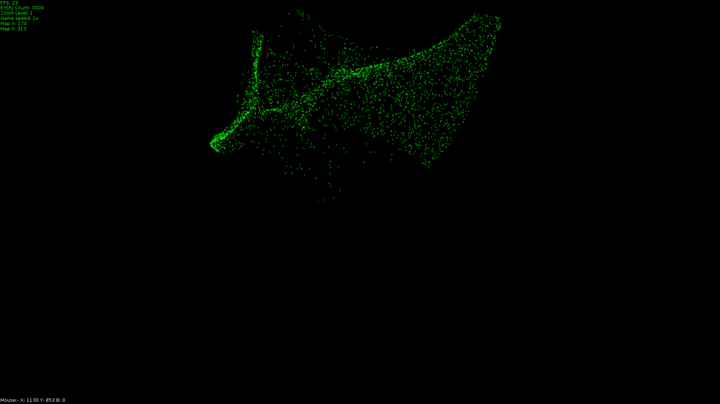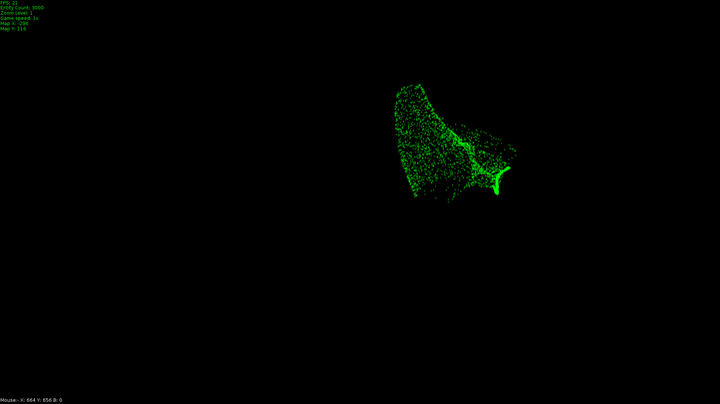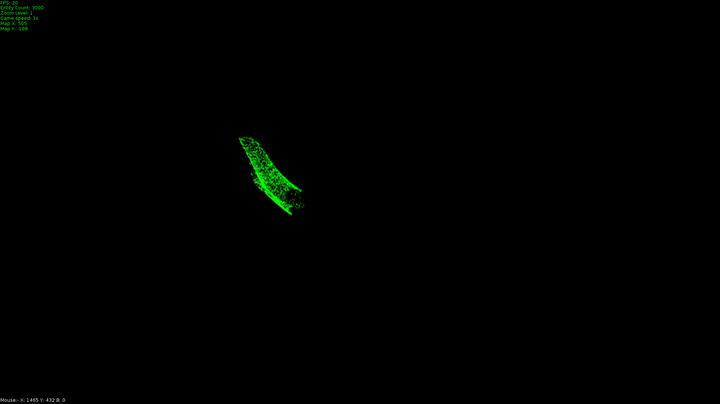
The dots in the program I made do just two things different to this in that they maintain their original velocity even when they get to their target. This is what leads to these swooping curves as they pass the target and have to start accelerating in a new direction. This is the second difference, these dots are always accelerating toward their target. I capped their top speed the same way we capped the acceleration vector, first I normalized their velocity and multiplied it by a value for top speed.
Leave a Comment
If you have any questions at all then please just let me know, I'll try to answer all of them. You can follow me here @pedrosgali. You don't have to, frankly I'm just glad you read this far. :)
I used to be fascinated by these type of effects in the demo-scene productions of yester-year... btw Did you ever follow the posts of the creator of Love, Eskil Steenberg?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I didn't, I will now though! Where did you read it?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Trying to understand this but my little brain just says 'no'. To be honest you lost me at Patrick Stewart, he's looking fine for 76! I'll continue to enjoy the pretty patterns and leave the clever stuff to you :-)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Beautiful maths by a beautiful boy x
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks Sammy. x
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This is a really great post! :D
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I featured your blog/work here on my post today:
https://steemit.com/steemit/@dragonanarchist/eyes-on-the-minnows-episode-2
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @pedrosgali! You have received a personal award!
Click on the badge to view your own Board of Honor on SteemitBoard.
For more information about this award, click here
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @pedrosgali! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit