Para desarrollar el determinante |A| de una A matriz de orden 3, 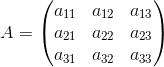 .
.
Usamos la fórmula:
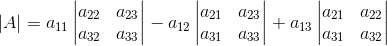
Busquemos el algoritmo que nos permita calcular el de terminante de una matriz de orden 3 de manera más directa:
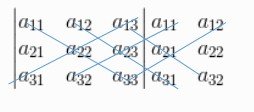
Las lineas en diagonal indican la sumatoria de los productos de los tres elementos que conforman la diagonal, de lo cual sale dos resultados:
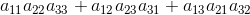
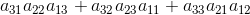
Para obtener el determinante de la matriz A (|A|) se toman estos dos resultados y se restan usando como minuendo la sumatoria de los productos obtenidos a través de la diagonal que va de arriba hacia abajo y como sustraendo lo que de manera análoga se obtuvo por vía de las diagonales que van de abajo hacia arriba.
Esto es:
|A|=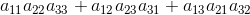 - (
- (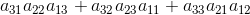 )
)
Ejemplo: Calcule el determinante de 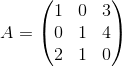
Aplicando el algoritmo que se acaba de explicar anteriormente, se amplía la matriz agregando a su derecha las dos primeras columnas y se desarrollan los productos en diagonal efectuando luego la diferencia entre los resultados de acuerdo al orden explicado anteriormente.
Esto es:
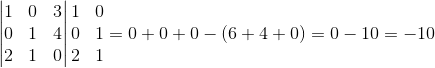
De esta manera se concluye que el determinante de la matriz A es -10
Una de las aplicaciones más importantes de los determinantes es la solución de Sistemas de Ecuaciones Lineales (SEL) con tres incógnitas.
Regla de Cramer:
Considérese el siguiente SEL:
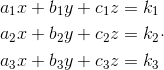
El cual se desea resolver para x , y y para z; para ello se construye la matriz de coeficientes del sistema, el cual es:
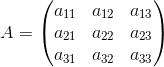
Y cuyo determinante es denotado por
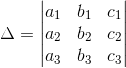
Sean
 ,
, 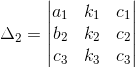 y
y 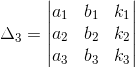 ; cada uno de los determinantes obtenidos al sustituir la columna correspondiente a cada variable por los valores del vector columna cuyas entradas corresponden a cada valor de k.
; cada uno de los determinantes obtenidos al sustituir la columna correspondiente a cada variable por los valores del vector columna cuyas entradas corresponden a cada valor de k.
La Regla de Cramer nos asegura que el valor de las variables x, y y z se obtienen a través del siguiente algoritmo:
 ,
, 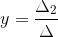 y
y 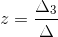
Si 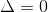 y
y 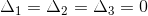 entonces el sistema tiene un número infinito de soluciones. Si
entonces el sistema tiene un número infinito de soluciones. Si 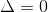 y
y 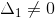 o
o 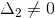 o
o 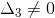 entonces el sistema no tiene ninguna solución.
entonces el sistema no tiene ninguna solución.
Ejemplo:
Dado el siguiente SEL: 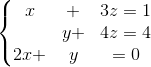
El determinante de la matriz asociada a este sistema ya fue calculado al inicio de este post: 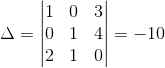
Siguiendo el mismo procedimiento calculemos 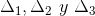
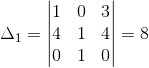 ,
, 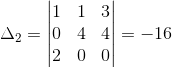 y
y 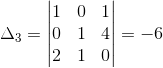
De donde:
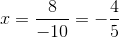 ,
, 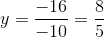 y
y 
Referencia:
Frank Ayres, JR.(1978). Matrices.McGraw-Hill
Jagdish C. Arya/Robin W. Lardner(1989). Prentice Hall Hispanoamericana S.A. México.
La matrices y los determinantes fueron creadas con la ayuda del Editor en línea de ecuaciones LateX.

¡Felicidades!
Proyecto Coonocimiento @proconocimiento reconoció tu esfuerzo
#humanidades, #ciencia, #arte y #tecnología.
Si quieres mantener nuestro voto usa nuestra etiqueta #proconocimiento
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit