
Hello. It is @hunhani.
Thank you for your interest and support in the previous posts. I will do my best to meet your expectations.
Last time, We have learned about how quantum parallelism due to quantum superposition and quantum entanglement relates to quantum communication security.
Chapter 4. Quantum Information Processing using Qubits This time, let's talk about what is the qubit and how does it used for quantum information processing.
 )
)Simple Review
Quantum parallelism is key.
- The superposition and entangled quantum states allow to manipulate all states in a single operation.
- Quantum parallelism enables quantum information processing, quantum communication, and quantum cryptography to solve problems that conventional computers can not solve.
It is impossible to copy any quantum states.
- Quantum mechanical information can not be copied perfectly.
- This allows us to establish a quantum key distribution cryptosystem that can not be absolutely stolen in communication security.
- External measurement action damages the quantum information sent by the sender, so the act of stealing information of sender/receiver is immediately detected
Quantum computers with both sides of communication security.
- A quantum computer poses a major threat to modern communications security that employs public key cryptography, while it can provide a quantum cryptography transmission method that is absolutely impossible to eavesdrop.

Qubit! Basic unit of quantum information
The word Qubit, which is the result of combining the bits of the classical information with the quantum in quantum physics, is the basic unit of quantum information. Unlike a bit consisting of either 0 or 1, the qubit adopts the appropriate quantum mechanical system and uses a new unit of information that can have 0 and 1 at the same time. The qubit information is mathematically described as a state in a two-dimensional vector space for complex numbers. Is it full of difficult words? Comprehension is faster than explaining in terms of space geometry.
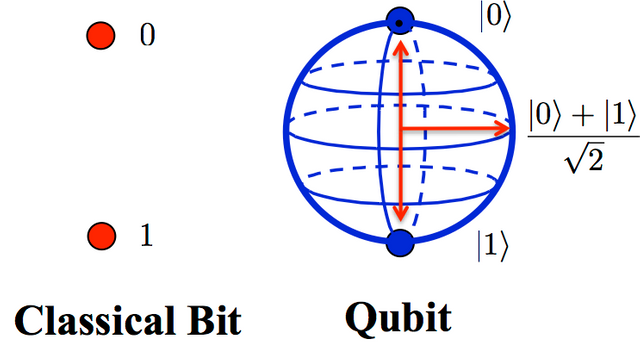
For the probabilistically expressed Bloch sphere where all possible events occur, the surface of the sphere consists of points where the sum of the probability values of the two different results is one. Classic bits can only have 1 and 0 values for the 'Arctic' and 'Antarctic' of the sphere, whereas the qubits exist anywhere in the sphere at the same time. If you have understood the quantum superposition and entanglement that I have been explaining, you would have guessed that the probabilities for both events 1 and 0 coexist on the remaining surfaces except the Arctic and Antarctic.
In this way, it is possible to have the effect of processing both 0 and 1 at the same time in the calculation process by using the fact that the qubit can have 0 and 1 at the same time. With this, quantum information processing using qubits can easily solve the problems that current supercomputers can not do. Even currently widely used public-key cryptography based on the fact that it is very difficult to decompose a large number of prime numbers can be solved easily. I mentioned this for a while last time.

Find the average value with only one operation!
There is something to be noted here. If you want to find out the average value through operations of tens of millions of cases using a qubit with quantum parallelism means that it is possible to find the average value in a single operation. It is important to Keep in mind that it does not mean that tens of millions of individual computed values are retrieved at once. To understand this point, it is necessary to compare the difference between probability calculation and quantum calculation.
For example, suppose you have n boxes and only one out of n boxes contains a ball. To find the box that contains a ball in a classic way, we have to open n boxes. On the other hand, quantum parallelism allows us to open the box only once. We can write down the number of the box you want to open and open the box corresponding to that number. Surely, it is necessary to make n number of possible boxes in quantum superposition/entanglement states before opening operation.

However, these things can be done in a similar way through probability algorithms instead of quantum algorithms. The probability algorithms use a method to open the box of the determined number after n number of coins are decided and all the number of the box is decided. It seems no big difference because the probability of opening each box is stochastically overlapped, and for each box the probability of opening the box and finding the ball is greater than zero. But, if we do this, if the number of boxes increases, the probability of finding the ball by opening the box becomes exponentially smaller.
Exactly the same refutation can be applied to quantum computers. The probability algorithm can produce a probabilistic nesting of all possible states, but doing so will result in an exponential decrease in the probability of each state. The quantum algorithms can also produce qubits of all possible states, but doing so will cause the probability amplitudes of each state to become exponentially smaller and consequently become meaningless algorithms. Of course, the technical such qubits in quantum superposition/entanglement states is possible in the distant future.

The quantum computer can offset the wrong answer and amplify the correct answer
Let's just say the most fundamental difference between a probability algorithm and quantum algorithm. The probability of probability algorithm can never be negative, but quantum mechanics's probability amplitude can be negative, and it can even be a complex number. The positive and positive numbers can not be offset, but positive and negative numbers can be offset. In addition, since the sum of the probabilities should be preserved as 1, if the square of the absolute value of the probability amplitude becomes 0, the amplitude of the state of some other state must be increased because the sum is preserved if the amplitude of the state is canceled.
If you open the box as a quantum mechanical system for the box problem in the example above, you can get a meaningful probability of which box the ball is in. Of course, this is a tremendous improvement over the classic results, but it's still a polynomial speed increase, not an exponential speed increase. If the problem to be solved does not have regularity, it is necessary to maximize the probability amplitude of the correct answer and to minimize the probability amplitude of the incorrect answer. Therefore, the quantum computer is technically ineffective for that kinds of problems.
However, things gonna be changed if there is a regularity in the problem to be solved with structure enabling offset. The prime factorization for the large number is typical problem**. In this case, quantum algorithms have an exponential speed improvement over the classically known best algorithms. Therefore, we should know that quantum computers, which are consuming high technical costs, can play an important role in areas where exponential speed can be achieved and can not just be universally used in all areas.

The attitude that we treat quantum computers
Now, did you understand that a quantum computer can quantify a number of cases with a small number of qubits, and that the behavior of qubits itself is indeterministic, so that we can get values for many results at once? In addition, do not forget that it is possible to quickly remove the wrong answer by offsetting the opposite state as we represent the quantum states with a probability wave function. But someone can think of the quantum computer which is expensive technically as skeptical because we can not expect exponential speed in some problems that does not have regularity.
We should understand that there is a big difference between the speed of quantum computer and that of regular computer in terms of their characteristic and application. There is no need to be disappointed with the quantum computer, which sometimes shows that there is little or no difference in speed compared to the regular computer. Therefore, even if a quantum computer is developed, we expect that all of the regular computers that we use will not become useless, but quantum computers and regular computers will start to help and compete with each other in maximizing their technical efficiency.

Next time, we will deal with technical challenges we have to overcome for the world of quantum information.
I want to deliver it as easily as possible, but this topic is very difficult for everyone. If you comment your question, I will reply to you as easily and concisely as I can.
The following chapter is introduced.
Chapter 5. Technological Challenges to Overcome for Quantum Information World
Please do not take your eyes off!

Previous Story
- [Quantum Computer & Blockchain Security] Chapter 0. Introduction
- [Quantum Computer & Blockchain Security] Chapter 1. Quantum computer! What the hell is different with ordinary computer?
- [Quantum Computer & Blockchain Security] Chapter 2. Magical phenomena of nature, Quantum Superposition & Entanglement
- [Quantum Computer & Blockchain Security] Chapter 3. Janus-faced quantum computer Quantum Parallelism and Quantum Communication Security
- [Next-generation Transportation] Hyperloop! Why is it so special?
- [Review] 18 Stories to See “Interstellar” Movie More Fun with Physics
- Engineer Dream Diodes with a Graphene Interlayer
- All images used in this post are from Google Images.
# YHH
Congratulations @hunhani! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPDownvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Invest in D-Wave. They are the ones who make the quantum PCs for Google, Lockheed Martin. It's $2 a share on the NASDAQ. If there was ever a chance to future proof yourself, this is it.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Agree. D-Wave is sure to be a very nice item in the future.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
quantum computers are crazy and don't understand it one bit. lol!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This topic would be difficult for everyone. How about reading the following posts.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Awesome.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks for the compliment.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit