What are zk-SNARKs?
Zcash is the first widespread application of zk-SNARKs, which is a new form of zero-knowledge cryptography. Zcash's privacy guarantee comes from the ability to block transactions, but it can still be verified as valid under the network consensus rules through zk-SNARK.
The abbreviation zk-SNARK stands for "Zero-Knowledge Succinct Non-Interactive Argument of Knowledge", and the pointed proof structure can prove the possession of certain information, for example, a key without revealing the information. , And there is no interaction between the prover and the verifier.
"Zero-knowledge" proof allows one party (the prover) to prove to the other party (the verifier) that the content of the statement is true and does not disclose any information beyond the validity of the statement itself. For example, considering the use of random number hashing, the prover can persuade the verifier that there is indeed a number with the hash value without revealing the content of the number.
In zero-knowledge "proof of knowledge", the prover can convince the verifier not only that the number exists, but that they actually know such a number and do not disclose any information about the number.
The "succinct" zero-knowledge proof can be verified within a few milliseconds, even for very large program declarations, the verification length is only a few hundred bytes. In the original zero-knowledge protocol, the prover and the verifier must communicate back and forth many times, but in the "non-interactive" structure, the prover sends a "proof" to the verifier, and the "proof" consists of a single message. At present, the only known zero-knowledge proof method that is non-interactive and short enough to be published to the blockchain has an "initial setup phase", which is generated by the prover and the verifier. The public reference string. We call this public reference string the public parameters of the system.
If someone can obtain the randomness secret used to generate these parameters, they will be able to create false proofs that look valid to the verifier. For Zcash, this means that malicious parties may create counterfeit coins. In order to prevent this, Zcash designed a multi-party program to generate public parameters. To learn more about the parameter generation program and see the precautions taken to prevent randomness issues (for example, the computer is generating public parameters), please visit the Paramgen page. To learn more about the math behind the parameter generation protocol, please read a blog post or a white paper on the subject.
How ZK-SNARKS is built in ZCASH
In order to have zero-knowledge privacy in Zcash, the function that determines that the transaction is valid according to the network consensus rules must return whether the transaction is valid, without revealing any information about its calculations. This is done by encoding some network consensus rules in zk-SNARKs. At a very high level, zk-SNARKs first transform what you want to prove into an equivalent form about knowing the solution of certain algebraic equations.
In the following chapters, we will briefly introduce how to convert the rules for determining valid transactions into equations, and then the equations can be evaluated on candidate solutions without revealing any sensitive information to the parties verifying the equations.
Calculation → Arithmetic Circuit → R1CS → QAP → zk-SNARK
To transform the transaction validity function into a mathematical representation, the first step is to decompose the logical steps into the smallest possible operations, thereby creating an "arithmetic circuit". Similar to a Boolean logic circuit, in which a program is compiled into discrete single steps, such as AND, OR, NOT, when a program is converted into an arithmetic circuit, it is decomposed into single steps, including addition, subtraction, multiplication and division (In special cases, we will avoid using division).
The following is an example of an arithmetic circuit that calculates the expression (a + b) (b c):
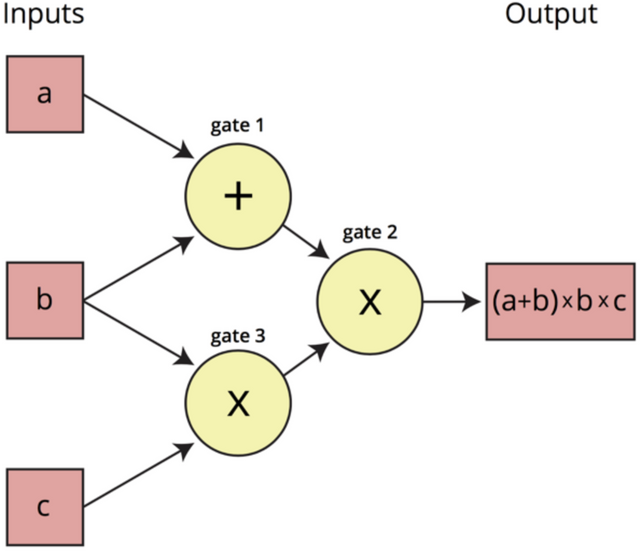
Looking at such a circuit, we can regard the input values a, b, and c as "traveling" from left to right on the output line. Our next step is to establish a Rank 1 Constraint System (Rank 1 Constraint System), namely R1CS, to check whether these values are "traveling correctly". In the above figure, R1CS will confirm that the value of the multiplication gate entered by b and c is b*c.
In this R1CS representation, the verifier must check many constraints-almost every line has a constraint. (Due to technical reasons, it turns out that we can only limit the lines that the multiplication gate leads.) In a 2012 paper on the subject, Gennaro, Gentry, Parno and Raykova proposed a good method to " All these constraints are combined into one". This method uses a circuit representation called the Quadratic Arithmetic Program (QAP). The single constraint that needs to be checked is between polynomials and not between numbers. The polynomial may be quite large, because when the identity between the polynomials does not hold, it will not be able to maintain the majority point. Therefore, you only need to check whether the two polynomials match at a randomly selected point in order to verify the proof correctly with a high probability.
If the prover knows in advance which point the verifier chooses to check, they may be able to create an invalid polynomial, but still satisfy the identity at the time. Using zk-SNARKs, complex mathematical techniques (homomorphic encryption and elliptic curve pairing) can be used to "blind" evaluation polynomials-that is, it is not known which point is being evaluated. The public parameters described above are used to determine which point will be checked and are in encrypted form so that neither the prover nor the verifier know what the public parameters are.
The description so far mainly deals with how to obtain the S and N in "SNARKs"-how to obtain short-lived, non-interactive single message proofs-but has not yet resolved what allows the "zk" (zero-knowledge) part of the prover to maintain its secret input Confidentiality. It turns out that at this stage, the "zk" part can be easily added by having the prover use a "random offset" of the original polynomial that still meets the required identity.
For an in-depth explanation of the key concepts behind zk-SNARKs in Zcash, please refer to the following blog post.
Zcash uses the libsnark branch, which is a C++ library for zk-SNARKs. You can check the code and learn more about the implementation on github. To learn more about the Zcash zk-SNARKs protocol, please refer to the Pinocchio protocol article.
How ZK-SNARKS is applied to create shielded transactions
In Bitcoin, transactions are verified by linking the sender address, recipient address, and input and output values on the public blockchain. Zcash uses zk-SNARKs to prove that the conditions for a valid transaction have been met, but did not disclose any important information about the address or value. The sender of the blocked transaction constructs an evidence that shows with high probability:
The sum of the inputs is equal to the sum of the outputs of each shield transition.
The sender proves that they have the private key entered, giving them the right to spend.
The entered private key is linked with the signature of the entire transaction. The link is encrypted, so the transaction will not be modified by those who do not know the private key.
In addition, blocked transactions must meet other conditions described below:
Bitcoin tracks (unspent transaction output) UTXO to determine which transactions are available. In Zcash, the shielded equivalent of UTXO is called a "commitment", and a spending promise includes exposing a "spending person". Zcash nodes keep a list of all commitments that have been created and all exposed spenders. Promises and invalid values are stored as hash values to avoid disclosing any information about the promise or which invalid values are related to which promise.
For each new banknote created by shielded payments, a promise will be announced containing a hash of the following:
Address to send banknotes
Amount sent
The unique number "rho" of this banknote (used to derive the spender later) and a random number.
Commitment = HASH(recipient address, amount, rho, r)
When a shielded transaction is spent, the sender uses their spending key to announce a spender who is a hash of a unique number ("rho") from an existing commitment that has not been used, and provides a zero-knowledge proof To prove that they have the right to spend it. The hash must not be in the spending list, which is stored in each node of the blockchain.
Nullifier = HASH(spending key, rho)
The zero-knowledge proof of shielded transactions confirms that in addition to the conditions listed above, the following determinations are also correct:
For each input, there is a clear commitment.
The consumer and the banknote promised to calculate the correct value.
There will never be any conflict between the consumer who outputs the banknote and the consumer of any other banknote.
In addition to the spending keys used to control addresses, Zcash also uses a set of proof and verification keys to create and check proofs. These keys are generated in the public parameter program discussed above and shared among all participants in the Zcash network. For each shielded transaction, the sender uses their certification key to generate proof that their input is valid. Miners check that the protected transactions follow the consensus rules by checking the prover's calculations using the verification key. The design method of Zcash proof generation requires the prover to do more work in advance, but it simplifies the verification, so the main calculation work is transferred to the creator of the transaction (this is why creating a shielded Zcash transaction may take up to 40 seconds, and at the same time It only takes a few milliseconds to verify that the transaction is valid).
The privacy of Zcash's shielded transactions relies on standard, proven cryptography (hash function and stream cipher), but it adds zk-SNARKs, which are used with the promise and spend mechanism to allow shielding the sender and receiver of the transaction Prove that encrypted transactions are effective. Other methods of providing privacy for cryptocurrencies rely on obscuring the links between transactions, but the fact that Zcash transactions can be stored in a fully encrypted blockchain opens up new possibilities for cryptocurrency applications. Encrypted transactions allow parties to enjoy the benefits of a public blockchain while protecting their privacy. The planned future upgrade will allow users to selectively disclose information about blocked transactions based on their own judgment. Check out the Zcash blog post on the near future to learn about Zcash’s future plans.
For a more in-depth explanation of how to build shielded transactions in Zcash, please refer to our blog post on how transactions between shielded addresses work. For complete details of the current Zcash protocol, please refer to our protocol specification.
Future applications of ZK-SNARKS
Creating shielded transactions in Zcash is just one example of the many possible applications of zk-SNARKs. In theory, you can use zk-SNARK to verify any relationship without divulging the input or leaking information. The amount of calculation for generating proofs of complex functions is still too large, and many programs are not yet applicable, but the Zcash team is pushing to optimize the boundaries of zk-SNARKs, and has created a new situation with more efficient implementation.