
Hello friends and followers of steem, welcome to my blog, this time in a challenge of the learnings provided to us in the form of homework by professor @khursheedanwar about equations and inequalities, all focused on teaching and learning algebra.
Professor @khursheedanwar explains us very well the concepts of equation and inequality, real life examples and some methods to find the solutions of equations and inequalities, so I think all this information is a correct guide to be able to perform the tasks.
Activity or task 1.
- Explain the difference between linear and quadratic equations. Provide examples of each type of equation and describe their general forms.
There are many differences between linear and quadratic equations, however, the ones that I consider most important are the following:
[1] The variable of higher degree in the linear equation is of first degree, while the variable of higher degree in a quadratic equation is of second degree.



[2] The linear equation will always have a solution, this means that there will always be a value for the first degree variable for which the equality is fulfilled, while in the second degree equation there will not always be two values of the second degree variable for which the equality is fulfilled, therefore the quadratic equation will not always have a solution.

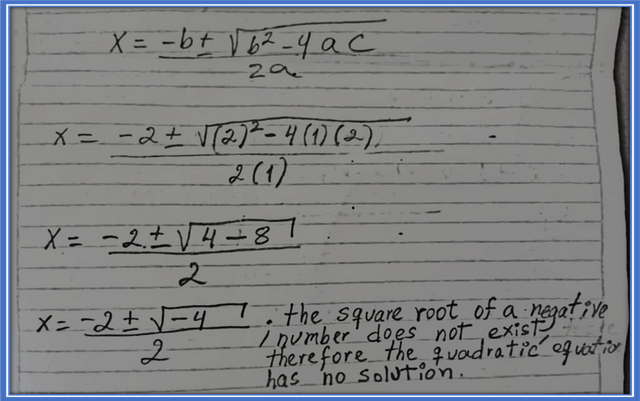
[3] In the case that the quadratic equation has a solution, the quadratic equation will have two solutions X1 and X2, while the linear equation will have only one solution.

As can be seen in the example shown, the two equations have a solution, the linear equation in order to comply with the equality it must be fulfilled that X = 10, and the quadratic equation in order to comply with the equality it must be fulfilled that X1 = -1 and X2 = -6.
The difference is that the linear equation has one solution and for this example the quadratic equation has two solutions.
Task 2
- Describe two different types of inequalities (not explained in the course). Provide examples of each type of inequality and explain how to solve them.
There are two types of inequalities that were not explained which are rational inequalities and absolute value inequalities, which are explained below:
Rational inequalities
They are rational because on both sides of the inequality there is a fraction, in which variables that can be of first degree or more can be found in the numerator or denominator, for example:

Below is an example of a video I recorded to explain them:
The other type of inequality that I am going to explain that was not explained in the introduction post of the challenge is absolute value inequalities.
Absolute value type inequalities are inequalities where following the properties of absolute value is paramount:
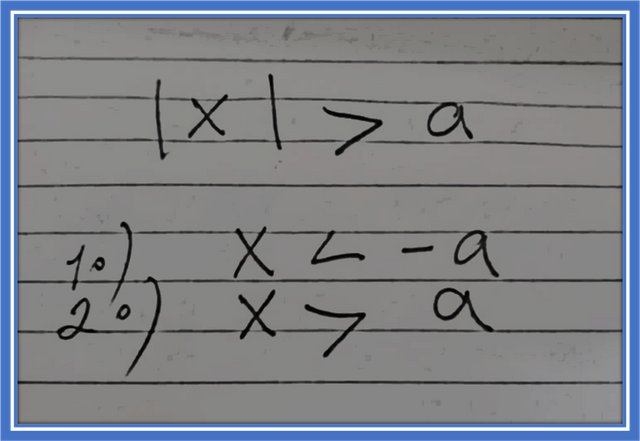
We are going to use this property of absolute value when solving this type of inequalities, it is important to mention that (a) has to be positive, otherwise it would be an empty set.
Next an example of inequality of the absolute value type:

To solve the example of the absolute value inequality shown above I am going to show you the following video where I explained its resolution:
Task 3
Solve the following linear equation: 2x + 5 = 11.Show step-by-step solution and share its practical example of how this equation can be applied in real life scenario.
(You are required to solve this problem at paper and these share clear photographs for adding a touch of your creativity and personal effort which should be marked with your username)
Well friends as my profession is petroleum engineer, I am going to put a little creativity in the resolution of this exercise, so to apply this equation 2x + 5 = 11 in a real life scenario I am going to write the following statement:
11 drill pipes are needed to complete drilling an oil well, but only 5 drill pipes are available at the location.
Knowing that twice the number of pipes plus 5 pipes in stock gives a total of 11 pipes, how many drill pipes are needed?
To solve this exercise it is necessary to know that the variable x is the amount of drill pipe needed to complete the 11 pipes needed in the drilling of the oil well, and as the double of the pipes plus 5 existing pipes add up to the 11 pipes needed, we could say that the equation that solves this exercise is the following:

Task 4
Scenario: Tom's Bakery
Tom's bakery is a most famous bakery of tow and it's famous for its yummiest pastries and bread. Tom which is owner want for making sure that he has sufficient ingredients for meeting needs for his famous chocolate cake and chocolate cake recipe needs 2 cups of flour, 1 cup of sugar and 1/2 cup of cocoa powder for each cake.
Equation
If Tom wants for making x cakes and he has 10 cups of flour, 8 cups of sugar and 4 cups of cocoa powder then calculate number of cakes that can be made by Tom?
Well friends to understand this exercise you have to divide the problem into two parts, first know Tom's recipe for each ingredient, for this you have:
- Flour: 2 cups.
- Sugar: 1 cup.
- Cocoa powder: 1/2 cup
Knowing that these are the ingredients you need for each cake.
The second thing to know is the ingredients that Tom actually has:
- Flour: 10 cups.
- Sugar: 8 cups.
- Cocoa powder: 4 cups.
We can calculate an equation for each ingredient, therefore the lesser number of all the ingredients will be the number of cakes that Tom can make, since the cake has all the ingredients and in the proportion of the recipe as stated in the exercise statement:
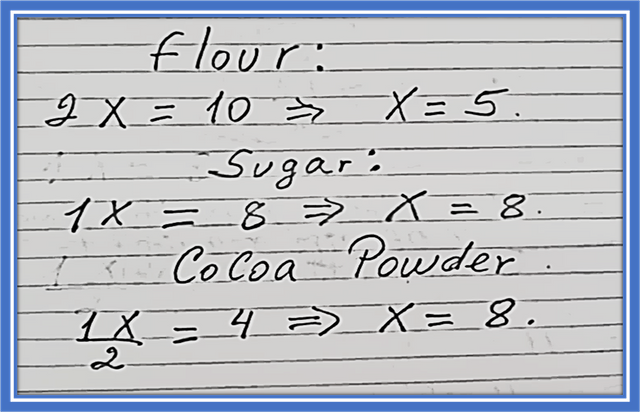
You can only make a total of 5 cakes, because if you could make a maximum of 8 cakes because there is enough sugar and cocoa powder, however you have to look for 6 cups of additional flour, but with the ingredients that Tom has available you can only make 5 cakes.
Inequality
Tom wants for making sure that he has sufficient sugar for meeting needs for his chocolate cake. He also knows that each cake needs 1 cup of sugar and he has 8 cups of sugar which are available. He also knows that he wants to make at least 6 cakes.
To express this part in the form of an inequality it is necessary to know that the variable X is quantity of cakes, we also know that Tom has 8 cups of sugar available, but he only wants to make 6 cakes, knowing that the recipe is 1 cup of sugar for each cake.
We ask ourselves:
What is the minimum number of pies Tom can make?
The minimum he can make is 6 cakes, since that is actually the amount he wants to make.
What is the maximum number of cakes Tom can make?
Even though Tom only wants to make 6 cakes, he can make a maximum of only 8 cakes if he wants to make them, since knowing that the recipe is 1 cup of sugar per cake, then if he has 8 cups of sugar he can only make a maximum of 8 cakes.
Therefore the inequality would be expressed as follows:

Scenerio: Number of gallons Ashley needs.
Suppose there's a person named Ashley who is planning for a road trip from City A to City B.If I talk about distance between two cities then it's around 240 miles. Ashley's car fuel tank have ability of holding 12 gallons of Suppose that his car gets 20 miles for each gallon then how many gallons of gas may Ashley purchase if he already has 2 gallons in his tank and he wants to have minimum 1 gallon left over when he arrives at City B?
Equation
Let's consider x as number of gallons of gas Ashley can purchase.
Para la ecuación debemos saber que la variable X es la cantidad de galones de gasolina que Ashley puede comprar, como ya Ashley tiene 2 galones de gasolina en el tanque de su automóvil, entonces la capacidad del tanque de gasolina del automóvil de Ashley es de 12 galones pero él solo quiere gastar 1 galón, entonces la cantidad de gasolina (x) + 2 galones que ya tiene, van a ser igual a 12 -1 galón, por lo que la ecuación queda:
X+2 = 11
para resolver restamos 2 a ambos lados de la igualdad:
X+2-2= 11-2
X=9
Lo que significa que el problema planteado en forma de ecuación nos hace concluir que solo necesita comprar 9 galones de gasolina.
Inequality
X + 2 ≥ (240/20) - 1
To find out the minimum amount Ashley needs to buy we solve the inequality:
Step 1: We divide 240 / 20 = 12, which implies that the inequality looks like this:
X + 2 ≥ 12 - 1
Second step: We subtract 12-1= 11, so the following expression remains:
X + 2 ≥ 11
Third step: We subtract -2 on both sides of the inequality:
X + 2 - 2 ≥ 11 - 2
Finally we have solved the inequality:
X ≥ 9
The minimum number of gallons of gasoline Ashley can buy is 9 gallons.