Hello friends and followers of algebra, in this opportunity sharing with all of you the challenge of the fourth week concerning linear and quadratic equations.
This time the teacher @khursheedanwar invites us to participate in this challenge in which basically we must perform the following tasks:
Task 1
• Explain difference between linear and quadratic equations. Provide examples of each type of system of equation and describe their general forms.
Comparison of Linear and Quadratic Equations
Most important differences
| Feature | Linear Equation | Quadratic Equation |
|---|---|---|
| Highest exponent of the variable | 1 | 2 |
| Shape of the graph | Straight line | Parable |
| Number of solutions | Generally a | You can have two, one or no real solution |
Linear Equations
- General form: The general form of a linear equation is ax + b = 0, where:
a and b are constant numbers (coefficients).
x is the variable.
Graph: The graph of a linear equation is always a straight line.
Examples:
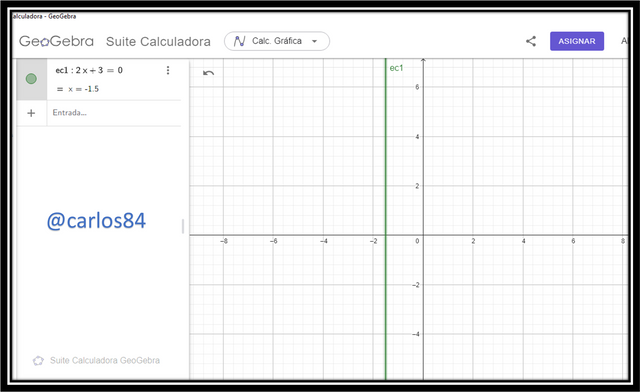
2x + 3 = 0
As we can see in the example above 2x + 3 = the variable x is raised to the power 1.
It can only have one solution:
2x + 3 = 0
2x=-3
x = -1.5
and its graph represents a straight line, as shown below:
- y = 5x - 2
In this example we simply express this linear equation in the form of a function f(x)=y, where if we make x=0 we find the y-intercept, and if we make y=0 we find the x-intercept.
y=5x-2
if x=0 implies that:
y=-2
So we get the point (0;-2).
If y=0 implies that:
5x-2=0 we clear the variable x
5x = 2
x = 2/5 = 0.4
So we obtain the point (2/5;0)
The graph is the following straight line:
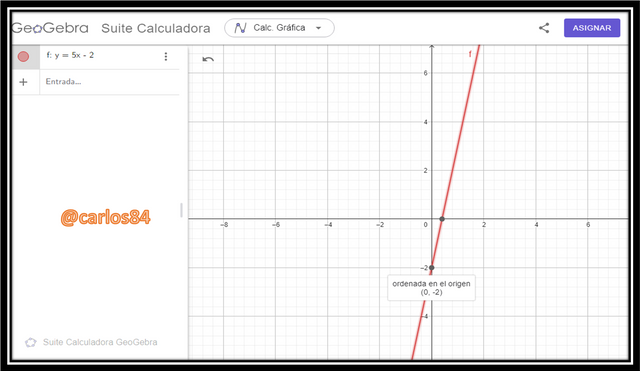
It is important to mention that when a straight line is expressed as a function where y=mx+b, each of the variables (x and y) will depend on each other.
Quadratic Equations
General form: The general form of a quadratic equation is ax² + bx + c = 0, where:
x is the variable.
a, b and c are constant numbers (coefficients), and a is nonzero.
a must be nonzero because if it is equal to zero the quadratic term is eliminated and it is no longer a quadratic equation.
- Graph: The graph of a quadratic equation is always a parabola.
What will vary is whether it opens on the x-axis or on the y-axis.
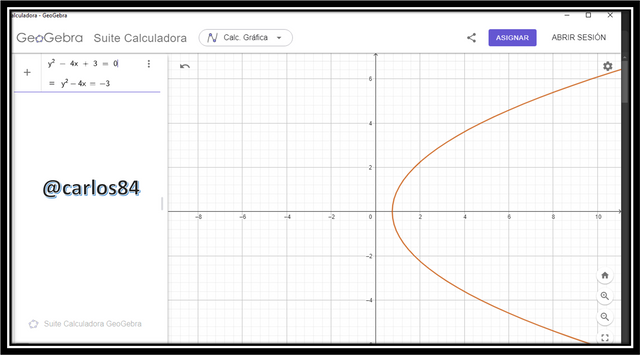
for example if it opens on the x-axis it is because it is an expression like this:
y² - 4x + 3 = 0
.
If it opens on the y-axis it is because it is such an expression:
y = 4x² + x - 1
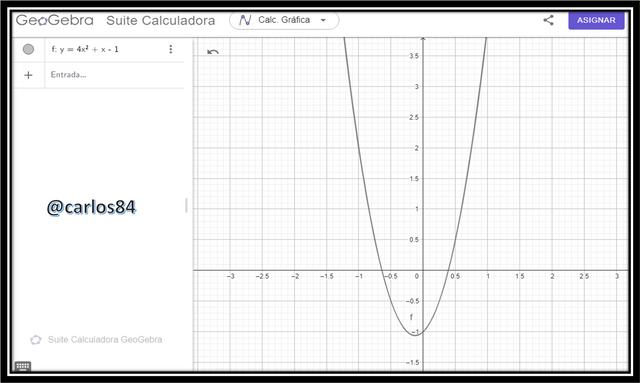
We have other examples of expression of quadratic equations:
Examples:
x² - 4x + 3 = 0
In the example above we have a second degree equation or also called a quadratic equation
which possibly has two solutions for x, in which we can factor to find its solution:
(x - 1 ) (x - 3 ) = 0
Therefore:
x-1 = 0
x = 1
x - 3 = 0
x = 3
The solution of the equation of second degree is x = 1 and x = 3
- y = 2x² + 5x - 1
In the previous example we have this quadratic function, for which we can find its graph and see what the solutions of the variable x are:
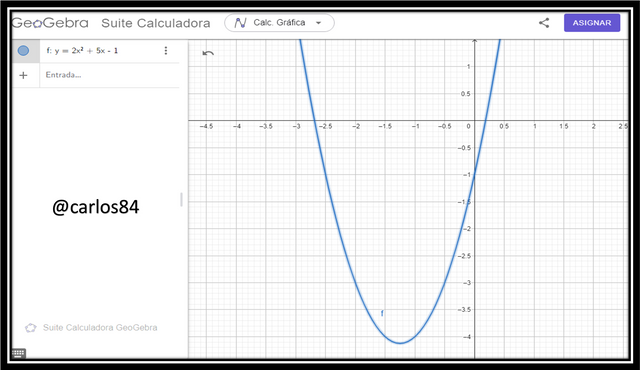
In the image above we can see that the parabola intercepts the x-axis at two values of x:
x = 0.186
x= -2.686
In the following example:
- -x² + 3 = 0
it can be seen that the quadratic equation lacks a term which is the linear term (bx) which is why we can find its solution by simply clearing x as follows:
-x² + 3 = 0
since x is negative we pass it to the other side of the equality in a positive form:
x² = 3
The square having as a power the variable x is passed to the other side of the equality in square root form:
x = √3
x =1.732
x = -1.732
In Summary
Linear and quadratic equations are two fundamental types of equations in algebra.
The main difference between them lies in the highest exponent of the variable, which in the linear equation is a straight line and in the quadratic equation is a parabola, and in the form of their graphs, since the linear equation represents straight lines, while the quadratic equation represents parabolas. .
Regarding the solutions, the linear equations will have only one solution and it will always have a solution, while the quadratic equation will have two solutions, but it may or may not have a solution.
• Task 2
• Describe methods for solving quadratic equations and share pros and cons for each method.
Methods for Solving Quadratic Equations
1. Factorización:
- Description: It consists of expressing the quadratic equation as the product of two binomials.
Example: (x - 3) (x + 2)
We know that this method works, because if we multiply the two binomials the resultant is a quadratic equation.
Advantages It is an efficient method when the factorization is easy to identify. It provides a direct understanding of the roots of the equation. As long as it can be applied it is not necessary to look for the solution of a quadratic equation by another method, since this is one of the simplest and easiest to apply.
Disadvantages: Not all quadratic equations can be easily factored, especially if the roots are not integers or if the equation has no real solutions.
2. Completing the square:
Description: The quadratic equation is transformed into a perfect square trinomial, which allows finding the roots by clearing the variable.
Advantages: It is a useful method for any quadratic equation and serves as a basis for the derivation of the general formula.
Disadvantages: It can be a tedious process and requires a series of algebraic steps.
3. General formula:
Description: It is a formula that directly provides the solutions of any quadratic equation of the form ax² + bx + c = 0.
of the form ax² + bx + c = 0.Advantages It is the most general method and it always works, regardless of the complexity of the equation. In my particular case it is the method I use the most to find the solution of quadratic equations.
Disadvantages: It can be more tedious than other methods if the coefficients are large or fractional numbers. However, if the person uses a calculator for the algebraic calculations, in the end the calculations involved in solving this method do not become difficult.
4. Graph:
Description: It consists of graphing the quadratic function and finding the points where the graph intersects the x-axis. These points correspond to the roots of the equation.
Advantages: It provides a clear visualization of the solutions and can be useful to understand the behavior of the function.
Disadvantages: It requires the precise construction of a graph, which can be laborious and not always accurate. However with the technological advancement of some applications and software such as Geogebra, we can easily graph. For example if we have
y = 3x² + 4x - 2
We graph with Geogebra software and we obtain:
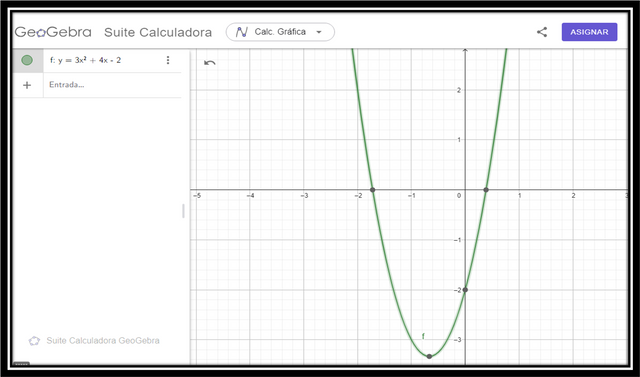
When to use each method?
Factorization: Ideal for quadratic equations with small coefficients and integer roots.
Completing the square: Useful when you need to express the equation in vertex form or when the factorization is not obvious.
General formula: The most general and reliable method for any quadratic equation.
As I told you before, this is the method I use the most to find the solution of a quadratic equation.
- Graph: Useful for visualizing solutions and for solving application problems where geometric interpretation is required.
Example
Let us solve the quadratic equation x² - 5x + 6 = 0 using different methods:
- Factorization: (x - 2)(x - 3) = 0, then x = 2 o x = 3.
- Completing the square: (x - 5/2)² = 1/4, then x = 5/2 ± 1/2, which gives x = 2 o x = 3.
- General formula: Using the formula x = (-b ± √(b² - 4ac)) / 2a, we obtain x = 2 or x = 3.
Given x² - 5x + 6 = 0, which of the three methods is the easiest to find the solution of this quadratic equation?
Logically that the factoring method is the easiest for this particular case, because if we think of two numbers that multiplied algebraically give me 6 which is the independent term and at the same time those two numbers give me -5 which is the linear term (bx), then we have to think of -2 and -3, therefore the factoring simply is: (x -2) (x -3) when we multiply the two binomials gives us the quadratic equation x² - 5x + 6 = 0, its solution is x = 2 and x = 3.
In conclusion, The choice of method to solve a quadratic equation depends on several factors, such as the complexity of the equation, personal preferences and the context of the problem. It is advisable to be familiar with all the methods in order to select the most appropriate one in each situation.
• Task 3
• Solve for linear equation 3x + 2 = 11 and show value of x?
• Solve for this quadratic equation x^2 + 2x - 6 = 0.
(You are required to solve these problems at paper and then share clear photographs for adding a touch of your creativity and personal effort which should be marked with your username)

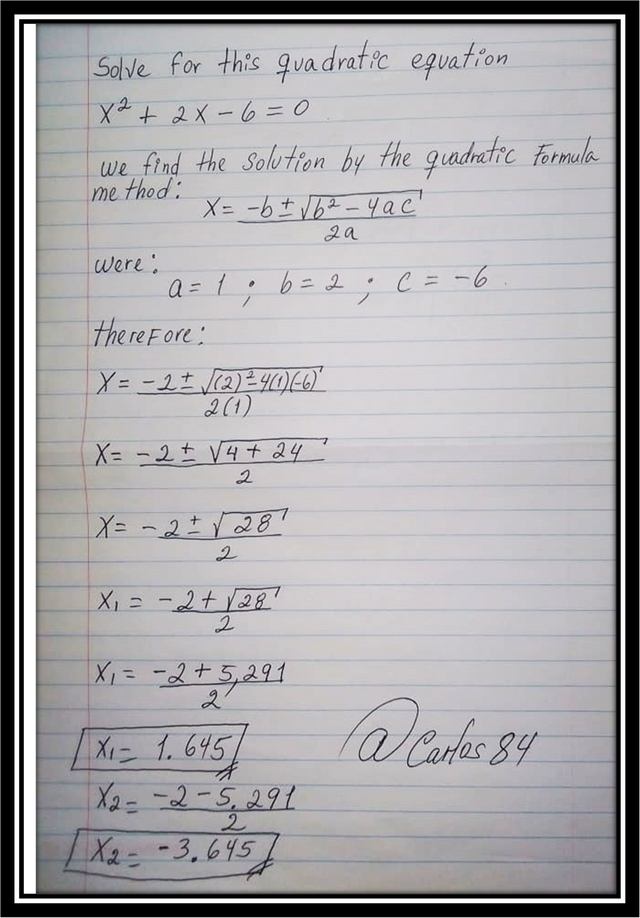
• Task 4
Scenario number 1
Suppose Ali have $15 for spending at snacks. He is buying a pack of chips for $3. How much money he have left?
Suppose x is amount of money Ali has left.
Equation: x + 3 = 15
Share a solution for x
(Solve the above scenerio based questions and share step by step that how you reach to your final outcome)
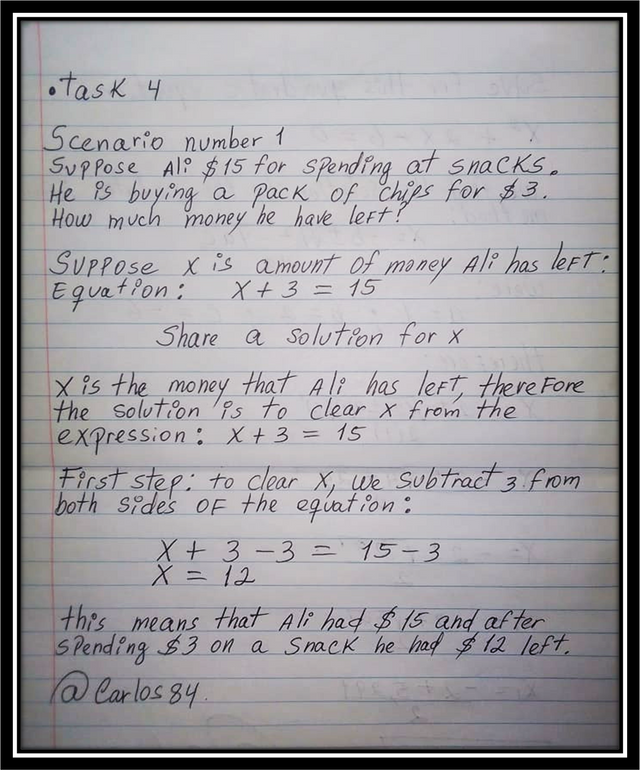
When solving the linear equation x +3 = 15 knowing that x is the amount of ali's money she has left after buying the package of potato chips at $3.
we clear x:
x = 15 -3
x = 12, which means that Ali after buying the snack (package of potato chips) has $12 left.
To find out if that really was what Ali had left, we substitute x = 12 into the original equation, and if it really satisfies the equality, it is because that really was what Ali had left after buying the packet of chips.
x + 3 = 15
12+3 = 15
15 = 15
Which means that really $12 was what Ali had left over after buying the package of potato chips.
Scenario number 2
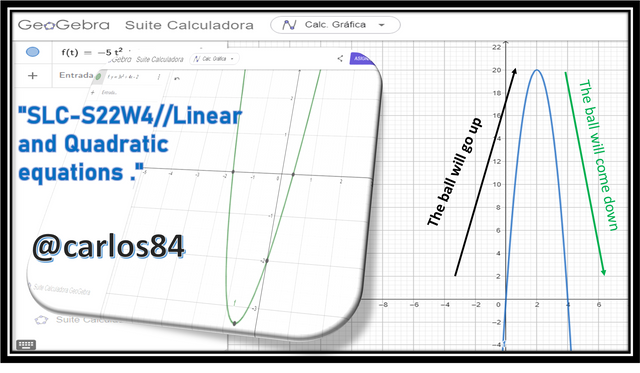
Suppose there's a ball which is thrown in upward direction from ground with initial velocity of 20 m/s and height of ball above ground is presented by following equation;
h(t) = -5t^2 + 20t
Here h is height in meters and t is time in seconds.
Share about maximum height reached by this ball!
Please solve for h!
Solution
Understanding the Equation:
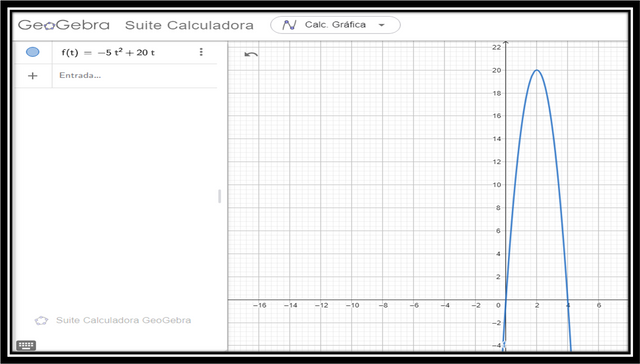
- h(t)=-5t²+20t: This equation represents the height of the ball as a function of time. It is a quadratic equation, which means that the graph of this function will be a parabola, as shown below:
- *-5t²: This term causes the parabola to open downward, indicating that the ball will rise and then fall.
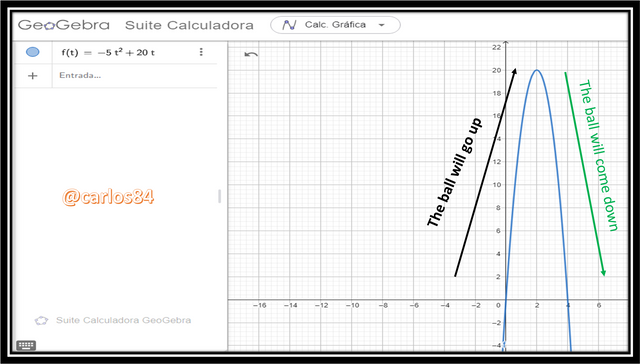
- 20t: This term represents the initial velocity of the ball.
Finding the Maximum Height:
The maximum height will be reached at the vertex of the parabola. To find the vertex of a parabola given by the equation y = ax² + bx + c, we use the formula for the x-coordinate of the vertex: x = -b / 2a.
In our case:
- a = -5
- b = 20
Then, the time in which the maximum height is reached is:
- t = -20 / (2 * -5) = 2 seconds.
Now, to find the maximum height, we substitute t = 2 into the height equation:
- h(2) = -5(2)² + 20(2) = -20 + 40 = 20 meters.
However, in the case that we do not want to calculate the maximum height (Ymax) found at the vertex of the parabola, we simply plot in geogebra, and we realize that the Y-coordinate of the vertex of the parabola is at 20, therefore the maximum height is 20 meters.
Another alternative solution in the case that we do not want to calculate the maximum height with either the vertex formula of x = -b / 2a or using graphs, is to find the first derivative of the function h(t)
h(t)=-5t²+20t, therefore
h'(t) = -10t + 20
Since the criterion of the first derivative says that the maximum point is where the first derivative equals zero, it implies that:
h'(t) = -10t + 20
-10t + 20 = 0, we clear t:
10t = 20
t = 20/10
t = 2 seconds, we substitute t = 2 seconds in the function
h(t)=-5t²+20t
h(2)=-5(2)²+20(2)
h(2)=-5(4)+ 40
h(2)=-20+40
h(2) = 20
This means that when the ball had been there for 2 seconds it reached the maximum height of 20 meters and then began to descend.
Reply:
The maximum height reached by the ball is 20 meters.
Physical Interpretation:
What this means is that the ball will reach its highest point of 20 meters above the ground within 2 seconds of being thrown. After that point, it will begin to fall again due to gravity.
Summary of the analysis and interpretation of the exercise:
Using the properties of quadratic equations and the concept of the vertex of a parabola, we have been able to determine the maximum height reached by the ball.
However, we have also seen how in a secondary way we have been able to apply other methods such as a graphical interpretation and finding the maximum point by means of the criterion of the first derivative to determine the maximum height (Ymax) = 20 meters.