SLC-S22W4 // Linear and Quadratic equations

_Fuente

Explicar la diferencia entre ecuaciones lineales y cuadráticas. Proporcionar ejemplos de cada tipo de sistema de ecuaciones y describir sus formas generales.

💠 Ecuaciones lineales.

Son ecuaciones algebraicas que operan solamente con sumas o restas de las variables cuyas potencias son iguales a 1. Existen diferentes características que las diferencian de las ecuaciones cuadráticas como son:

• El grado.
  Las ecuaciones lineales son también denominadas ecuaciones de primer grado o grado 1, pues sus variables tienen valores exponenciales igual a 1.


• La forma.
  Tienen la forma general:
  
  a₁x₁+ ... + a_nx_n + b = 0
  
  donde, a₁ + ... + a_n son los coeficientes de la ecuación , suelen ser números reales y al menos uno de ellos debe ser distinto de cero. También pueden ser parámetros o expresiones algebraicas que no contengan ninguna de las variables.
  
  x₁ + ... + x_n son las variables o incógnitas de la ecuación.
  
  b es el término independiente de la ecuación y puede ser cero.
  
  Comúnmente estas ecuaciones suelen tener una o dos incógnitas como las siguientes formas:
  

  ax + b = 0
  a₁x₁+ a₂x₂ + b = 0
  

  
  
• Representación gráfica.
  La representación gráfica de una ecuación lineal en el espacio bidimensional (x,y) es una línea recta y en espacio tridimensional (x,y,z) representa un plano.
  
  Por ejemplo:
  

  2x + y + 10 = 0
  2x + y + z + 1 = 0

  Las podemos representar en los siguientes planos.
  
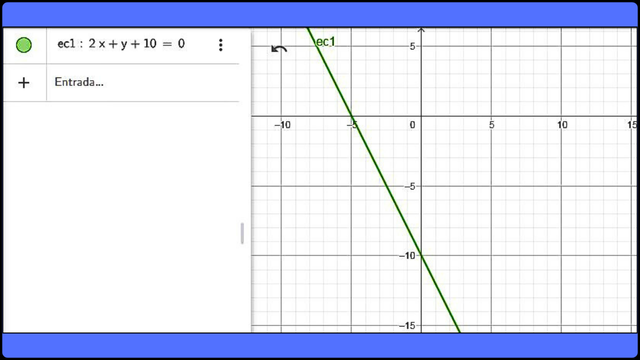  <sub>Representación gráfica de la ecuación lineal 2x + y +10 = 0 en el espacio bidimensional Fuente
  
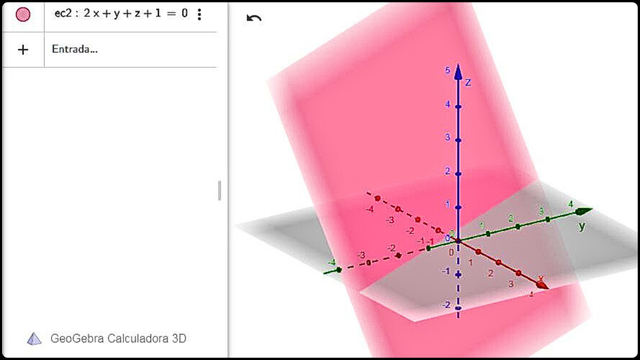  Representación gráfica de la ecuación lineal 2x + y + z + 1 = 0 en el espacio tridimensional Fuente</sub>


• Soluciones.
  En general, la solución de una ecuación lineal representa al conjunto de valores que cumplen con la ecuación. Es decir, al sustituir dichos valores en las variables de la ecuación hacen que la igualdad se cumpla.
  
  En el caso de una ecuación lineal con una variable, la solución es única siempre que el coeficiente que acompañe a la variable sea distinto de cero.
  
  Cuando la ecuación lineal cuenta con dos variables, estamos hablando de coordenadas cartesianas cuyo conjunto representan todas las soluciones de esta ecuación lineal. Por tanto, todos estos puntos forman una línea en el plano bidimensional.


• Ejemplo algebraico.
  

  Tenemos la ecuación 2x+y+10 = 0, determinar dos puntos solución de dicha ecuación lineal.

  Podemos determinar dos puntos solución, uno que corta la abscisa y otro que corta la ordenada, como sigue:
  
  Si x = 0 , tenemos: (2)(0) + y + 10 =0
  Restamos 10 a cada lado: y = -10
  
  Por tanto, el primer punto solución es P₁ = (0;-10)
  Si y = 0 , tenemos: 2x + (0) + 10 =0
  Restamos 10 a cada lado: 2x = -10
  Dividimos por 2 cada lado: x = -10/2
  
  Por tanto, el segundo punto solución es P₂ = (-5;0)
  
  Respuesta.
  Los dos puntos solución de la ecuación lineal son:
  P₁ = (0;-10)
  P₂ = (-5;0)


• Ejemplo práctico.
  

  Después de cancelar a Juan un sueldo “x” y a Pedro un sueldo “y” restan $200 en la caja. Establezca la ecuación lineal para que la caja quede vacía.

  El total de la caja (S) debe ser la suma de los sueldos de Juan (x) y Pedro (y) más el resto de $200, por tanto se puede definir esta relación con la siguientes ecuación lineal:
  
  S = x + y + 200
  
  Para que la caja quede vacía S = 0 y la ecuación se transforma en:
  
  x + y + 200 = 0
  
  Por tanto, esta es la ecuación lineal para que la caja quede vacía.

💠 Ecuaciones cuadráticas.

Son aquellas ecuaciones de segundo grado de una sola variable cuya potencia máxima es igual a 2. Tienen otras características que las diferencian de las ecuaciones lineales como:

• El grado.
  Las ecuaciones cuadráticas son también denominadas ecuaciones de segundo grado o grado 2, es decir el exponente máximo de la variable es igual a 2.


• La forma.
  La ecuación cuadráticas en general tiene la forma:
  
  ax² + bx + c = 0
  
  donde,
  a y b son los coeficientes de la variable en la ecuación. El valor de a debe ser distinto de cero.
  c es el término independiente de la ecuación.
  x es la variable en la ecuación.


• Representación gráfica .
  Las ecuaciones cuadráticas están representadas gráficamente por curvas parabólicas.
  
  Veamos que resulta al graficar a 2x² + 4x – 4.
  
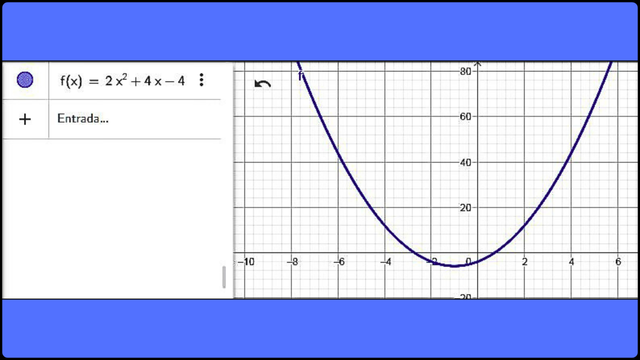  _{Representación gráfica de la ecuación cuadrática 2x² + 4x – 4 en el espacio bidimensional Fuente}
  Note que la curva de la gráfica es cóncava debido a que el signo del coeficiente de la variable x², es positivo. Si fuera negativo la curva de la gráfica sería convexa.
  
  También se pueden visualizar dos puntos de corte o raíces de la curva con el eje de las abscisas cuando la ecuación es cero así como el corte en la ordenada cuando x es igual a cero. En este caso, el extremo más bajo también es un punto típico de esta curva donde la pendiente es cero.


• Soluciones.
  Las soluciones de una ecuación cuadrática suelen ser dos con coeficientes reales o complejos, llamadas raíces, no necesariamente distintas.
  
  La solución puede obtenerse a través de la fórmula general:
  
  x = [-b ± √(b²-4ac)] / (2a)
  
  donde “x es la variable de la ecuación, “a” y ”b” son los coeficientes de las variables, y “c” el término independiente de la ecuación.
  
  Existen otros métodos para resolver las ecuaciones cuadráticas: factorización y completar el cuadrado.


• Ejemplo algebraico.
  Resolver la ecuación cuadrática 2x² + 4x - 4 = 0.
  
  Utilizando la fórmula general indicada en el punto previo, tenemos que:
  
  x = [-b ± √(b²-4ac)] / (2a)
  
  donde, a = 2; b = 4; c = -4, por tanto sustituimos y operamos matemáticamente:
  
  x = [ -4 ± √(4²-4(2)(-4) ] / (2(2)), simplificando tenemos:
  x = [ -4 ± √(16 +32) ] / 4, simplificando el paréntesis
  x = [ -4 ± √(48) ] / 4, simplificando la fracción
  x = -1 ± √48 / 4, ingresamos el 4 en la raíz
  x = -1 ± √(48/16), simplificamos la raíz
  x = -1 ± √3, simplificamos la raíz
  
  Soluciones:
  

  x₁ = -1 + √3
  x₂ = -1 - √3



• Ejemplo práctico.
  

Juan dispara un proyectil que sigue una trayectoria parabólica que se rige por la siguiente ecuación:

h = 0.7Vt - 4.9t²

donde,
h = es la variable de altura o posición vertical del proyectil
t = es la variable del tiempo del recorrido
V es la velocidad inicial: 2 m/seg

¿Cuánto tiempo tarda el proyectil en caer al suelo desde su lanzamiento?

Cuando el proyectil toca el suelo h = 0, entonces la ecuación del movimiento a resolver se transforma en:

0.7Vt - 4.9t² = 0

Factorizando tenemos: (t)(0.7V - 4.9t) = 0
Separamos el primer factor del segundo e igualamos a cero

t = 0, es la primera solución de la ecuación.

(0.7V - 4.9t) = 0, sumamos 4.9t en cada lado
4.9t = 0.7V, dividimos por 4.9 ambos lados
t = (0.7V/4.9), simplificamos la fracción y sustituimos el valor de V = 2 m/seg
t = (0.14)(2)

t = 0.28 seg, es la segunda solución de la ecuación

Solución.
Tenemos dos valores de t pero sólo uno responde a la pregunta. ¿Cuánto tiempo tarda el proyectil en caer al suelo desde su lanzamiento?

Desde su lanzamiento transcurrieron 0.28 seg para que el proyectil cayera al suelo.

Describe métodos para resolver ecuaciones cuadráticas y comparte los pros y los contras de cada método.

Existen diferentes métodos para resolver las ecuaciones cuadráticas y que se describen a continuación:

💠 Método de factorización.

Definición.
Consiste en expresar una ecuación cuadrática de la forma ax² + bx + c = 0 como un producto (ix +m)(jx + n) = 0, donde i, j, m y n, son valores a determinar por simple inspección.

Por tanto, (ix + m) = 0 ó (jx + n) = 0. Al resolver estas ecuaciones lineales se determinan las raíces de la ecuación cuadrática..

En la forma general cuando el coeficiente a es distinto a 1, la factorización por inspección se hace muy difícil, excepto en casos especiales cuando b o c son cero. También funciona solo para ecuaciones cuadráticas con raíces racionales.

Si a = 1, la forma x² + bx + c = 0 se factoriza como (x +m)(x + n) = 0, por tanto hay que encontrar los valores de m y n que al sumarlos sea igual a b y cuyo producto sea igual a c.

Ejemplo
Resolver por factorización la ecuación: x² + 2x - 8 = 0

Siendo b = 2 y c = - 8 debemos cumplir que:
m + n = 2
(m)(n) = - 8

Los valores de m y n se pueden ensayar con los divisores de c = - 8: ±1, ±2, ±4, ±8

Probamos sustituyendo m = 4 en (m + n) = 2 y tenemos: 4 + n = 2
Restamos 4 a ambos lados: n = - 2

Sustituimos n y m en (m)(n) = - 8 y tenemos: (4)(-2) = - 8
Se comprueba: - 8 = - 8

Por tanto, la ecuación factorizada es: (x + 4)(x - 2) = 0

Entonces se debe cumplir que:
(x + 4) = 0, por tanto x = - 4
(x - 2) = 0, por tanto x = 2

Solución:
Las raíces son (x₁; x₂) = (-4; 2).

Ventajas.

• Suele resolverse fácilmente para valores enteros de raíces de números reales
• Puede proporcionar una solución rápida cuando no tiene término independiente
• Ayuda a comprender e interpretar geométricamente las raíces de la ecuación.

Desventajas.

• Presenta mucha más dificultad que otros métodos cuando el coeficiente a es distinto de 1, lo que implica mucho más ensayos.
• La gran mayoría de las ecuaciones cuadráticas que corresponden a aplicaciones prácticas de la física no pueden resolverse por factorización
• Suele ser más lento cuando las raíces no son enteras, el proceso de ensayo y error aumenta.
• No siempre se puede factorizar en números racionales
• Requiere familiarizarse con la técnica de factorización y práctica.

💠 Método de completación de cuadrados.

Definición.
Consiste en un recurso de álgebra elemental que permite convertir la forma cuadrática general ax² + bx + c = 0, en otra equivalente de la forma:

a(x + j)² + k = 0, donde “k” es una contante.

Se pueden seguir los siguientes pasos:

1. Divide ambos lados de la ecuación por a
2. Resta el término independiente resultante (c/a) en ambos lados
3. Suma [(b/a)/2]² en ambos lados.
4. Expresar el lado izquierdo como cuadrado perfecto y simplifica el lado derecho
5. Igualar la raíz cuadrada del lado izquierdo con las raíces cuadradas del lado derecho
6. Resolver las dos ecuaciones lineales

Ejemplo.
Resolver por completación de cuadrados la ecuación:

2x² + 4x - 16 = 0

1. Divide ambos lados de la ecuación por a = 2: x² + 2x - 8 = 0
2. Resta el término independiente resultante (-c/a = 8) en ambos lados: x² + x = 8
3. Suma [(b/a)/2]² = 1 en ambos lados: x² + 2x +1 = 8 + 1
4. Expresar el lado izquierdo como cuadrado perfecto y simplifica el lado derecho: (x + 1)² = 9
5. Igualar la raíz cuadrada del lado izquierdo con las raíces cuadradas del lado derecho: (x + 1) = ±√9
6. Resolver las dos ecuaciones lineales:
   (x + 1) = ±√9 = ±3
   x = ±3 -1
   

Soluciones:

x₁ = 2
x₂ = -4

Ventajas.

• Se puede utilizar para la resolución de cualquier ecuación cuadrática sin importar si se puede factorizar o no.
• Permite reescribir la ecuación cuadrática para hallar su vértice y trazar el gráfico

Desventajas.

• Puede resultar tedioso el cálculo cuando los números no son enteros
• Suele requerir más pasos que otros métodos, por tanto requiere más tiempo comparativamente
• Requiere familiaridad y práctica con expresiones algebraicas.

💠 Por fórmula General.

Definición.
Como lo hemos detallado en la tarea anterior, las soluciones de una ecuación cuadrática suelen ser dos con coeficientes reales o complejos, llamadas raíces, no necesariamente distintas.

Existe una fórmula general que genera las soluciones explícitas de esta ecuación como sigue:

x = [-b ± √(b²-4ac)] / (2a)

donde “x es la variable de la ecuación, “a” y ”b” son los coeficientes de las variables, y “c” el término independiente de la ecuación.

Ejemplo.
Resolver por fórmula general la ecuación: x² + 2x - 8 = 0

Tenemos que x = [-b ± √(b²-4ac)] / (2a)

Siendo a = 1; b = 2 y c = -8 , sustituimos en la fórmula:
x = [-2 ± √(2²-4(1)(-8)] / ((2)(1))
x = [-2 ± √(4+32)] / 2
x = [-2 ± √(36)] / 2
x = [-2 ± 6] / 2, simplificamos la fracción

x = (-1 ± 3)

Soluciones:

x₁ = 2
x₂ = -4

Ventajas.

• Se utiliza para resolver cualquier ecuación de segundo grado, tanto en el campo de números reales como en los complejos.
• Es el método más popular para la resolución de la ecuación cuadrática.
• Proporciona soluciones exactas y directas.
• Es el mejor método cuando no se puede resolver con la factorización

Desventajas.

• Los cálculos son tediosos cuando los coeficientes no son números enteros
• Se puede incurrir en errores de cálculo por lo que debe ser más cauteloso con los resultados, por lo que deben comprobarse las raíces obtenidas

💠 Método gráfico.

Definición.
Consiste en graficar la función, expresada en la ecuación, en un plano bidimensional (x;y) dando valores a la variable y así obtener un conjunto de puntos o pares cartesianos que definen el dibujo o gráfico de la parábola que representa la ecuación cuadrática.

Normalmente se detectan las raíces en el eje de las abscisas, el corte en la ordenada y el extremo de la parábola, como los más característicos en este tipo de ecuaciones.

Ejemplo.
Determinar gráficamente las raíces de la ecuación: x² + 2x - 8 = 0

Se ubican varios puntos en la gráfica tomando la función de la ecuación:

f(x) = x² + 2x – 8

Punto A: x = -4, f(-4) = 16 +2(-4) - 8 = 16 -16 = 0
Punto B: x = 2, f(2) =4+2(2) – 8 = 4 + 4 – 8 =0
Punto C: x= -1, f(-1) = 1 +2(-1) -8 = -9
Punto D: x = 0; f(0) = - 8

Dibujando los puntos A(-4;0), B(2;0), C(-1;-9) y D(0;8) obtenemos la gráfica.

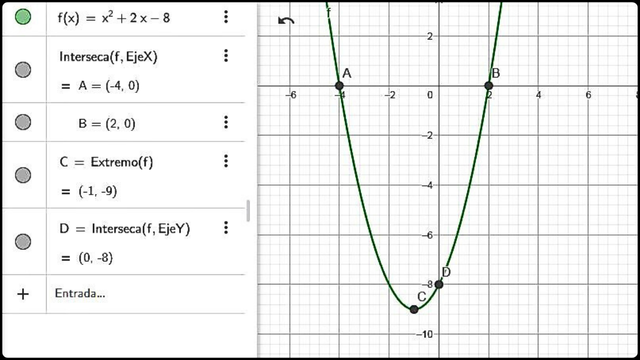_{Gráfica de la función cuadrática x² + 2x – 8 Fuente}
Ventajas.

• Es un buen método para visualizar la parábola y sus puntos de intersección
• Existen calculadoras gráficas en línea que facilitan su visualización muy rápidamente con gran precisión
• Las curvas obtenidas por calculadoras gráficas generan versatilidad, facilidad de modificar, mejorar nuestra capacidad analítica, nuestro diseño y presentación de resultados.
• La gráfica tiene una ventaja didáctica para la enseñanza que alimenta la compresión en los estudiantes sobre todo con el uso de la tecnología y calculadoras gráficas

Desventajas.

• No siempre es preciso cuando se dibujan manualmente.
• Es más lento cuando se dibujan manualmente

💠 Resuelve la ecuación lineal 3x + 2 = 11 y muestra el valor de x?

• Tenemos: 3x + 2 = 11
  Restamos 2 a ambos lados: 3x +2 - 2 = (11 - 2)
  Simplificando tenemos: 3x = 9
  Dividimos por 3 ambos lados: x = 9/3


• Solución: x = 3
  
  

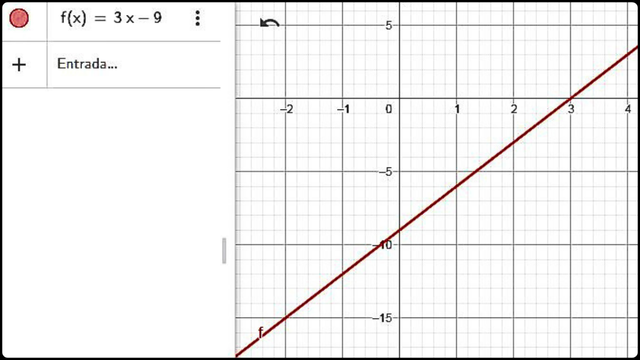_{Representación gráfica de la ecuación lineal 3x +2 = 11 Fuente}
En esta gráfica la línea nos permite ver los puntos de cortes con la abscisa y ordenada que pueden revelar soluciones al problema estudiado.

_{Resolución manual de la ecuación 3x + 2 = 11}

💠 Resuelve esta ecuación cuadrática x² + 2x - 6 = 0

Resolvemos aplicando la fórmula x = (-b ± √(b²-4ac))/2a

Tenemos:
a= 1, b= 2, c= -6

x = (-2 ± √(2²-4(1)(-6))/2(1)
x = (-2± √(4+24))/2
x = (-2 ± √28)/2
x = -1 ± √(28)/2
x = -1 ± √(28/4)
x = -1 ± √7

Soluciones:

x₁ = -1 + √7
x₂ = -1 - √7

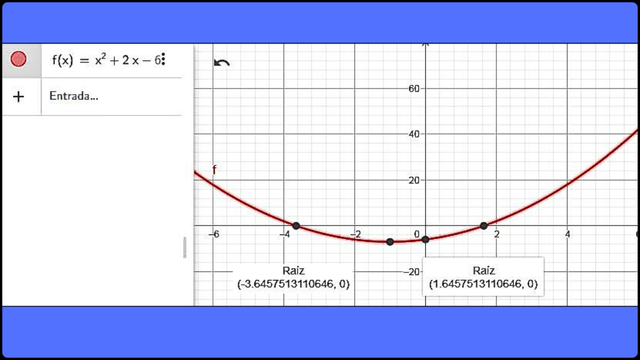_{Representación gráfica de la ecuación x² + 2x - 6 = 0 Fuente}

Esta gráfica es de gran ayuda para entender la ecuación y detallar las raíces de la misma.

_{Resolución manual de la ecuación x² + 2x - 6 = 0}

💠 Escenario número 1.

Supongamos que Ali tiene 15 $ para gastar en bocadillos. El ha comprado un paquete de patatas fritas por 3 $. ¿Cuánto dinero le queda?

Supongamos que x es la cantidad de dinero que le queda a Ali.

Ecuación: x + 3 = 15

Comparte una solución para x

• Tenemos: x + 3 = 15
Restamos 3 a ambos lados: x +3 - 3 = (15 - 3)
• Simplificando tenemos: x = 12

Respuesta.
El dinero que le queda a Ali son $12

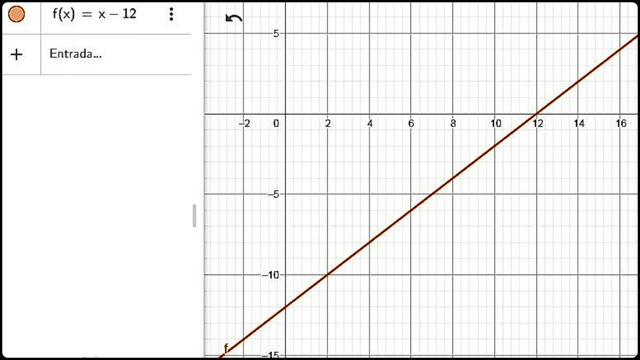_{Representación gráfica de la ecuación y = x+3 -15 Fuente}

En esta gráfica la línea nos permite ver los puntos de cortes con la abscisa y ordenada que pueden revelar soluciones al problema estudiado.

💠 Escenario número 2,

Supongamos que hay una bola que se lanza en dirección hacia arriba desde el suelo con una velocidad inicial de 20 m/s y la altura de la bola sobre el suelo se presenta por la siguiente ecuación;

h(t) = -5t² + 20t
Aquí h es la altura en metros y t es el tiempo en segundos.

Comparte la altura máxima alcanzada por la pelota.

Resuelve h.

El movimiento de la pelota está representado por una ecuación cuadrática o parábola. Cuando llega a su altura máxima, la pendiente de la curva en dicho punto es horizontal o igual a cero, siendo el punto de inflexión en la trayectoria.

Ese punto se define como la derivada de la ecuación, por tanto se cumple que:

(2at + b) = 0 donde a = - 5 y b = 20 para nuestro caso particular. Por tanto podemos hallar el valor de t cuando la pelota llega a la altura máxima (h)

Tenemos: (2at + b) = 0

• Restamos b a ambos lados: 2at = -b
• Dividimos por 2a ambos lados: t = -b/(2a)
• Sustituimos los valores de a y b: t = -20/[(2)(-5)]
• Simplificando t = (-20)/(-10)

Por tanto, t = 2 seg cuando la pelota alcanza su máxima altura. Entonces sustituimos en la ecuación del movimiento y determinamos el valor de la altura máxima.

Tenemos: h(t) = -5t² + 20t

Si t = 2 entonces h_max = -5(2)² + 20(2)
Simplificando h_max= -(5)(4) + 40
Resultando que h_max= - 20 + 40 = 20

Solución:
La máxima altura (h_max) alcanzada por la pelota son 20 m.

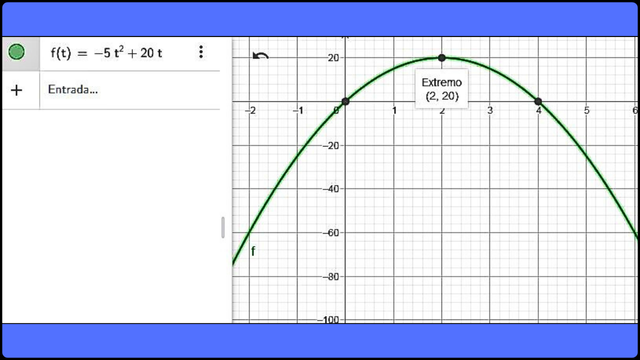_{Representación gráfica de la ecuación h= -5t² + 20t Fuente}
En la curva se puede observar el punto máximo de inflexión (2;20) en el cual sucede el cambio de pendiente. La simetría de este tipo de gráfica permite captar entre las raíces de la abcisa el valor de t = 2 para el cual sucede la altura máxima y en la odenada podemos apreciar el valor máximo de la función h = 20.

Notas:

📌 Imágenes presentadas con la aplicación canva.com
📌 Invito a participar a mis amigos @ridwant @paholags @marito74 @genomil @cruzamilcar63 @dasudi @dove11 @goodybest
📌 Más información del concurso en el siguiente enlace.
📌 Mi twitter: steemit_casv

Saludos a @khursheedanwar

¡Gracias por su visita!