SLC-S22W6 // Graphing and conic sections

Tarea 1.
Diferencia entre funciones cuadráticas y exponenciales con ejemplos y formas generales de cada una.

La diferencia esencial entre una función cuadrática y exponencial está en la ubicación de la variable dentro de la ecuación. Es decir, cuando la variable con el mayor exponente es igual a 2, estamos hablando de una función cuadrática o de segundo grado. Cuando la variable se ubica en el exponente de la ecuación entonces es una función exponencial.

Existen otras características que las diferencian y que explico a continuación:

💠 Funciones cuadráticas.

La función cuadrática está representada gráficamente por una curva parabólica simétrica con un vértice o extremo. Tiene la siguiente forma general:

f(x) = ax² + bx + c

Donde,

• “x” es la variable
• “a”,”b” y “c” son números reales donde “a” es diferente de cero.
• “2” es el grado mayor de la variable “x”
• “f(x)” es la función dependiente de “x”

Ejemplos de funciones cuadráticas:

• f(x) = 2x² + x +1
• g(x) = x² +5
• h(t) = ½ Gt²
• E(c) = mc²

Ejemplo de representación gráfica de la función f(x) = 2x² + 8x -12.

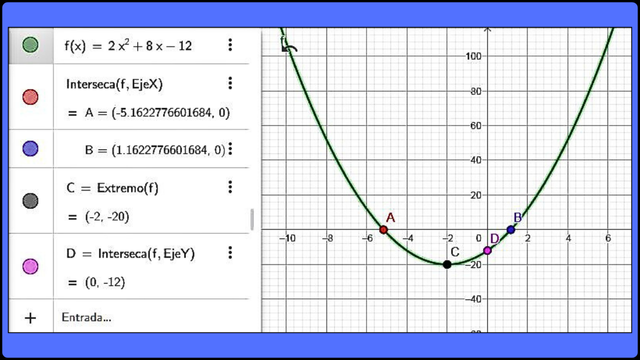_{Representación gráfica de la función f(x) = 2x² + 8x -12 F}
💠 Funciones exponenciales

Las funciones exponenciales gráficamente son curvas asimétricas con fuerte crecimiento exponencial y relacionado a la función logaritmo. Esta funciones tienen la siguiente forma general:

f(x) = ab^x

Donde,

• “a” es el coeficiente.
• “b” es la base de la función exponencial. Deber ser un número real mayor a 0 y distinto de 1. Cuando b>1 es una función creciente y cuando b<1 la función es decreciente.
• “x” es la variable y a su vez el exponente de la base “b”.
• “f(x)” es la función exponencial dependiente de “x”.

Ejemplos de funciones exponenciales:

• f(x) =2^x - 1
• g(x) = e^(x+1)
• h(t) = 4^{(x2 + 2)}

Ejemplo de representación gráfica de la función f(x) = e^x - 2.

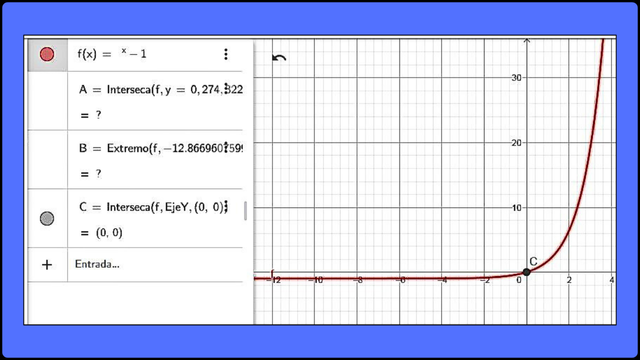_{Representación gráfica de la función f(x) = e^x-1 F}
Esta función exponencial es creciente por cuanto el valor de la base es mayor a 1.

Tarea 2.
Proporcione ejemplos reales de funciones exponenciales y cuadráticas (mínimo 2 para cada una) que no se hayan tratado en clase.

💠 Ejemplos de funciones exponenciales

Ejemplo 1.
La Ley de enfriamiento de Newton establece que la tasa de pérdida de calor de un cuerpo es proporcional a la diferencia de temperatura entre el cuerpo y su entorno. Viene expresada por la siguiente función exponencial:

T(t) = T_a + (T_o - T_a) e^-kt
Donde,

• “T_a” es la temperatura ambiente.
• “T_o” es la temperatura inicial del cuerpo.
• “k” es la constante de proporcionalidad.
• “t” es la variable tiempo.
• “T(t)” es la temperatura del cuerpo en función del tiempo “t”.

En la actualidad el enfriamiento newtoniano es considerado en modelos climáticos por ser computacionalmente menos costosa y rápida para calcular la temperatura atmosférica, muy útil para la predicción de acontecimientos de fenómenos naturales.

Veamos el siguiente ejemplo real:

Tenemos un pastel que sale del horno a 120ºC exponiéndose a la temperatura ambiente de 25ºC. Después de 3 minutos de enfriamiento, determine cuál es la temperatura del pastel aplicando la Ley de enfriamiento de Newton, si la constante de proporcionalidad es de 0.08.

Tenemos:

• Temperatura inicial del pastel T_o= 120ºC.
• Temperatura ambiente T_a= 25ºC.
• Constante de proporcionalidad k= 0.08.

Sustituimos estos parámetros en la función de La Ley de enfriamiento de Newton:
T(t) = T_a + (T_o - T_a) e^-kt
T(t) = 25 + (100 - 25) e^-0.08t

T(t) = 25 + 75e^-0.08t

Si t = 3 min, tenemos:
T(3) = 25 + 75e^-0.08(3)
T(3) = 25 + 75e^-0.24
T(3) = 25 + (75)(0.7874)
T(3) = 25 + 59.055
T(3) =84.055ºC ✔

Solución.
Después de 3 minutos de enfriamiento la temperatura del pastel es de 84.055ºC.

Representación gráfica de T(t) = 25 + 75e^-0.08t

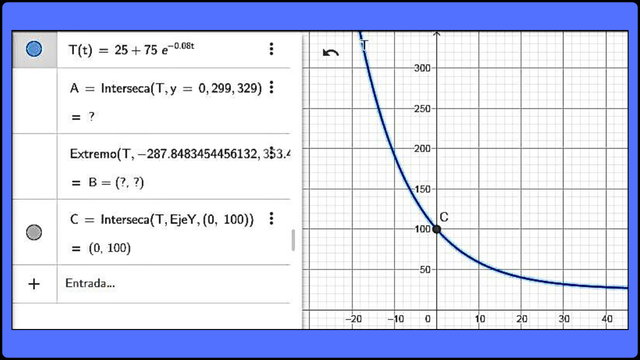_{Representación gráfica de la función T(t) = 25 + 75e^-0.08t F}
En este caso, la función es una curva decreciente.

Ejemplo 2.
En economía se puede calcular el capital actual partiendo de un capital inicial a una tasa de interés compuesto continuo después de transcurrir un período de tiempo. Para este fin, es muy utilizada la siguiente función exponencial:

C(t) = C_oe^it
donde,

• “C_o” es el capital inicial.
• “e” es el número de Euler.
• “i” es la tasa de interés.
• “t” es el tiempo transcurrido.
• “C(t)” es el capital actual que depende del tiempo “t”.

Veamos el siguiente ejemplo real:

Juan invierte un capital de $ 2000 a una tasa de interés compuesto continuo del 8% anual. ¿Determine el monto del capital de Juan al cabo de 10 años?

Tenemos que C(t) = C_oe^it
donde,

• C_o= $2000
• i = 8%
• t= 10 años

Sustituyendo en la función tenemos:
C(t) = 2000e^0.08t
C(10) = 2000e^(0.08)(10)
C(10) = 2000e^0.80
C(10) = (2000)(2.2255)
C(10) = 4.451 ✔

Solución.
Al cabo de 10 años, Juan obtuvo un capital de $4.451.

Representación gráfica de C(t) = 2000e^0.08t

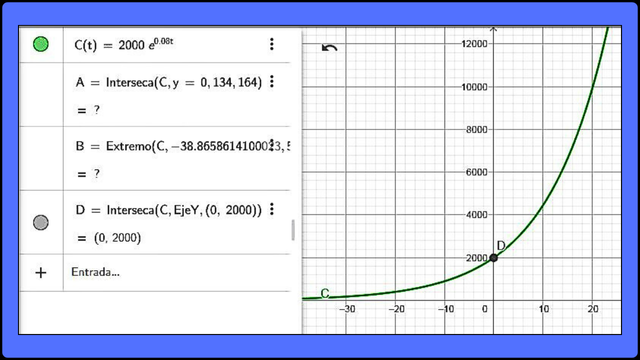_{Representación gráfica de la función C(t) = 2000e^0.08t F}
Esta curva nos muestra su carácter creciente para un capital inicial de $2000 a una tasa del 8% continuo durante un período de 10 años.

💠 Ejemplos de funciones cuadráticas

Ejemplo 1.

En un circuito eléctrico tenemos dos resistencias conectadas en paralelo R₁ y R₂. Se conoce que la resistencia R₂= R₁+4 y que la resistencia total requerida R_T son 6 Ohms.
Si se cumple que 1/R_T = 1/R₁ + 1/R₂, determine el valor de las dos resistencias que cumplan dicha relación.

Lo primero que debemos hacer es sustituir el valor de R_T y R₂ en la relación de las resistencias como sigue:

1/6 = 1/R₁ + 1/(R₁ + 4)

Determinamos el mínimo común múltiplo (m.c.m.) de las fracciones como: 6R₁(R₁ + 4).
Multiplicamos ambos lados de la ecuación por el m.c.m. y simplificamos:

6R₁(R₁ + 4)/6 = 6R₁(R₁ + 4)/ R₁ + 6R₁(R₁ + 4)]/ (R₁ + 4)
R₁(R₁ + 4) = 6(R₁ + 4) + 6R₁
R₁² + 4R₁ = 12R₁ + 24
R₁² + 4R₁ - 12R₁ - 24 =0

R₁² - 8R₁ - 24 =0

Esta es la ecuación cuadrática a resolver por la fórmula general:

R₁ = [-b ± √(b²-4ac)] / (2a), donde a= 1, b= -8 y c= -24.

Por lo tanto,
R₁ = [8 ± √(-8²-4(1)(-24)] / (2(1))
R₁ = [8 ± √(64+96)] /2
R₁ = [8 ± √(160)] /2
R₁ = 4 ± 6.32
R₁ = 4 + 6.32 = 10.32 ✔
R₁ = 4 - 6.32 = -2.32. (La resistencia negativa no es válida)

Por tanto, R₁ = 10.32 Omhs. ✔

Tenemos que R₂ = R₁ + 4 = 10.32 + 4

Por tanto, R₂ = 14.32 Omhs. ✔

Comprobamos que se cumple: 1/R_T = 1/R₁ + 1/R₂

1/6 = 1/10.32 + 1/14.32 = 0.1667
0.1667 = 0.0969 + 0.0698
0.1667 = 0.1667 ✔
Cumple ok…!

Representación gráfica de la función cuadrática R₁² - 8R₁ - 24 =0

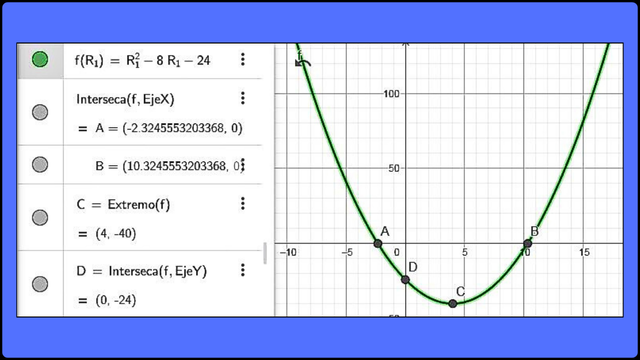_{Representación gráfica de la función R1² - 8R1 - 24 =0 F}
Ejemplo 2.

Se deja caer una bola desde lo alto de un edificio de 100 m de altura. Determine cuanto tiempo tarda en alcanzar el suelo si la aceleración de la gravedad es 9.8 m/seg².

El movimiento se identifica como una caída libre, por lo cual parte del reposo cumpliendo la siguiente función cuadrática del movimiento vertical:

h(t) = (1/2)gt²

Donde,

• t = tiempo recorrido en la trayectoria
• h(t) = altura de la caída recorrida en el tiempo “t”= 100 m
• g = aceleración de la gravedad = 9.8 m/seg².

Entonces, sustituimos los valores en la función y simplificamos como sigue:

-100 = -(9.8/2)t²
(2)(100) = (9.8)t²
t² = (2)(100)/9.8

t = ± √20.408 = ± 4.52 ✔

Solución.
El tiempo no puede ser negativo, por tanto t = 4.52 segundos. Es decir, la bola tarda en llegar al suelo en 4.52 segundos.

Representación gráfica de la función cuadrática h(t) = - (1/2)gt²

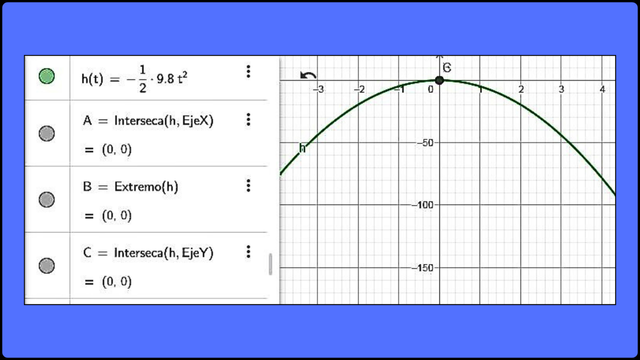_{Representación gráfica de la función h(t) = -(1/2)gt² F}

Tarea 3.
Hallar la ecuación de la circunferencia con centro (2, 3) y radio 4.

La ecuación ordinaria de una circunferencia viene dada por la expresión:

(x-a)² + (y-b)² = r²

Donde,

• “a” y “b” son la abscisa y la ordenada del centro de la circunferencia.
• “r” es el radio de la circunferencia.
• “x” y “y” son puntos de la circunferencia.

Por tanto, si el centro es (2,3) tenemos que a =2 y b = 3. Si el radio r =4 entonces, sustituimos estos valores en la ecuación ordinaria y la desarrollamos para hallar la ecuación general como sigue:

(x-2)² + (y-3)² = 4²

Desarrollamos y simplificamos:
x² + 2x(-2) + (-2)² + y² + 2y(-3) +(-3)² = 16
x² - 4x + 4 + y² - 6y + 9 = 16
x² + y² - 4x - 6y + 13 = 16
x² + y² - 4x - 6y + 13 - 16 = 0

Solución.
x² + y² - 4x - 6y - 3 = 0 es la ecuación de la circunferencia con centro (2,3) y radio 4.

_{Resolución de la ecuación de una circunferencia con centro (2,3) y radio 4}
Representamos gráficamente x² + y² - 4x - 6y - 3 = 0, a continuación:

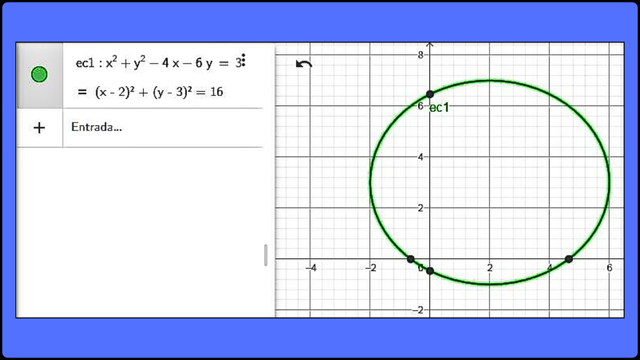_{Representación gráfica de x² + y² - 4x - 6y - 3 = 0 F}

Hallar x: 2x² + 5x - 3 = 0

Se trata de una ecuación cuadrática cuya solución se encuentra en las raíces que pueden ser determinadas por la fórmula general.

x = [-b ± √(b²-4ac)] / (2a)
donde,

• “x” es la variable de la ecuación cuadrática.
• “a” es el coeficiente que acompaña a la variable de segundo grado.
• “b” es el coeficiente que acompaña a la variable de primer grado.
• “c” es el término independiente.

Por tanto, a= 2, b= 5 y c= -3. Entonces, procedemos a sustituir en la fórmula general para hallar las soluciones a la ecuación, como sigue:

x = [-5 ± √(5²-4(2)(-3)] / (2(2))
x = [-5 ± √(25 + 24)] / 4)
x = [-5 ± √49] / 4)
x = -5/4 ± 7/4

x₁ = -5/4 + 7/4 = 2/4 = 1/2 = 0.50 ✔
x₂ = -5/4 - 7/4 = -12/4 = - 3 ✔

Las soluciones son:

x₁ = 0.50
x₂ = -3

Comprobación:

2x² + 5x - 3 = 0, para x= 0.50 tenemos:

2(0.5)² + 5(0.50) - 3 = 0
(2)(0.25) + 2.50 - 3 = 0
0.50 + 2.50 - 3 = 0
3 - 3 = 0 ✔
Cumple ok..!

2x² + 5x - 3 = 0, para x= - 3 tenemos:

2(-3)² + 5(-3) - 3 = 0
(2)(9) - 15 - 3 = 0
18 - 15 - 3 = 0
3 - 3 = 0 ✔
Cumple ok..!


Veamos gráficamente la ecuación 2x² + 5x - 3 = 0

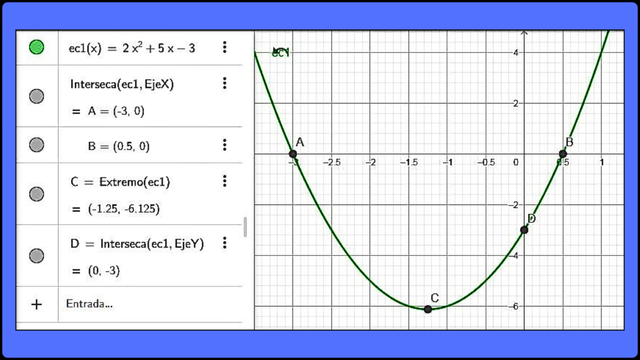_{Representación gráfica de 2x² + 5x - 3 = 0 F}

Tarea 4.
Escenario número 1.

Si la ecuación del paraboloide viene dada por y = 0,1x², entonces x e y se miden en metros;

a) Es necesario representar gráficamente esta ecuación.
b) Averiguar la distancia focal del paraboloide.
c) Necesitas encontrar la ecuación de la directriz.

a) Gráfico de la ecuación.
Para representar gráficamente una ecuación paraboloide en el plano cartesiano es necesario conocer algunas características y algunos puntos clave por donde trazar la curva. Entre ellos está el vértice (V), el foco (F) y los puntos extremos del lado recto (LR) de la parábola.

En este caso particular, la ecuación del paraboloide y = 0,1x² tiene la forma canónica:

x² = 4py, donde “p” es la distancia focal.

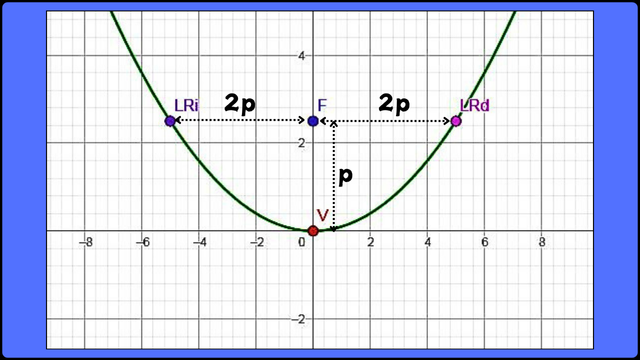_{Punto claves para graficar una parábola vertical con vértice en el origen F}
Es una ecuación típica de una parábola cuyo vértice (V) se localiza en el origen de coordenadas, su eje de simetría es paralelo a la ordenada, su foco (F) se localiza en el eje de simetría a una distancia (p) desde el vértice (V), su lado recto (LR) mide 4p y es perpendicular al eje de simetría, de tal manera que la parábola es una curva convexa o abre hacia arriba.

Por tanto, ya tenemos el vértice V(0,0). El punto focal se ubica arriba de éste en F(0,p) por que debemos determinar la distancia focal (p).

Tenemos y = 0,1x², despejamos el lado derecho e igualamos a la ecuación canónica definida anteriormente como sigue:

x² = 10y
x² = 4py
10y = 4py
10 = 4p
p = 10/4 = 2.50 ✔

Por tanto, p = 2.50. La distancia focal es 2.50 metros.

Entonces tenemos F(0,2.50). ✔ Por lo tanto, el lado recto (LR) = 4p= 10 metros ✔. Con esto tenemos sus extremos izquierdo y derecho respectivamente, LR_i y LR_d, por lo que cada uno mide 2p= 5 metros desde F(0,2.50). De allí definimos la ubicación de dichos puntos como sigue:

LR_i(-5,2.50) ✔
LR_d(5,2.50) ✔

En resumen tenemos los puntos V(0,0), F(0,2.50), LR_i(-5,2.50) y LR_d(5,2.50), con los cuales podemos dibujar la curva en el plano cartesiano como sigue:

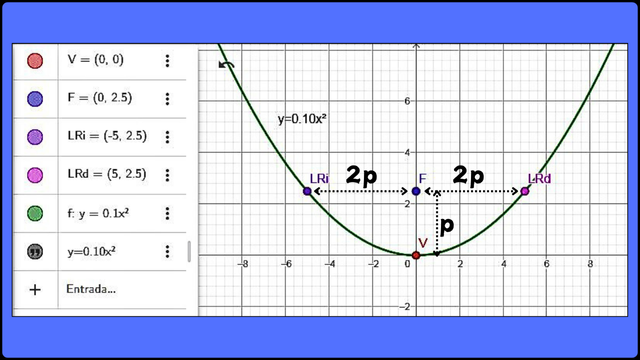_{Representación gráfica de y = 0,1x² F}
Elementos de la parábola.

Para complementar el conocimiento y proseguir con las respuestas de los literales b) y c) de la presente tarea, es necesario conocer los siguientes elementos de una parábola que nos permiten comprender mejor la gráfica que pretendemos obtener.

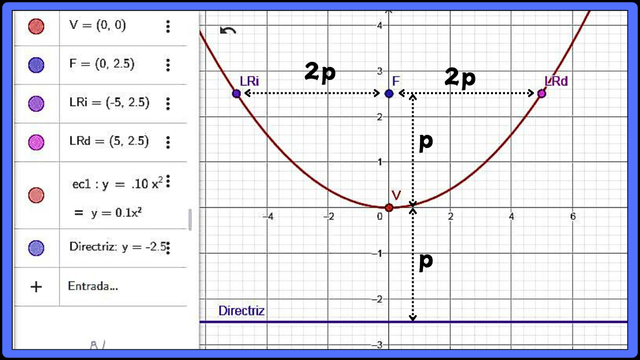_{Elementos de la parábola F}
Vértice (V). Es el punto donde la parábola cruza su eje de simetría. También se le denomina el extremo de la parábola como el punto máximo o mínimo de la curva.

Foco (F). Es el punto fijo ubicado en el interior de la parábola en el eje de simetría a una distancia (p) desde el vértice.

Directriz (D). Es la línea perpendicular al eje de simetría ubicada fuera de la parábola a una distancia (p) desde vértice (V) o 2p desde el punto focal (F).

Eje de simetría. Es una línea recta que pasa por el vértice (V) y el foco (F), dividiendo a la parábola en dos partes iguales.

Distancia focal (p). Es la distancia que hay desde el vértice (V) al foco (F) y desde el vértice (V) a la directriz (D).

Lado recto (LR). Es la recta perpendicular al eje de simetría que pasa por el foco (F) hasta tocar la curva de la parábola. Mide 4p de extremo a extremo y 2p desde el extremo al foco(F).

Ecuación canónica. Las parábolas son curvas con infinidad de posiciones y orientaciones dentro de un plano cartesiano. Las siguientes ecuaciones canónicas están simplificadas considerando la particularidad cuando el eje de simetría es paralelo a algunos de los ejes cartesianos.

Así tenemos parábolas verticales u horizontales con el foco (F) ubicado arriba, abajo, a la derecha o a la izquierda del vértice (V).

Para el vértice V(h,k) tenemos:

(y-k)² = 4p(x-h) parábola horizontal abriendo a la derecha.
(y-k)² = -4p(x-h) parábola horizontal abriendo a la izquierda.
(x-h)² = 4p(y-k) parábola vertical abriendo hacia arriba (convexa).
(x-h)² = -4p(y-k) parábola vertical abriendo hacia abajo (cóncava).

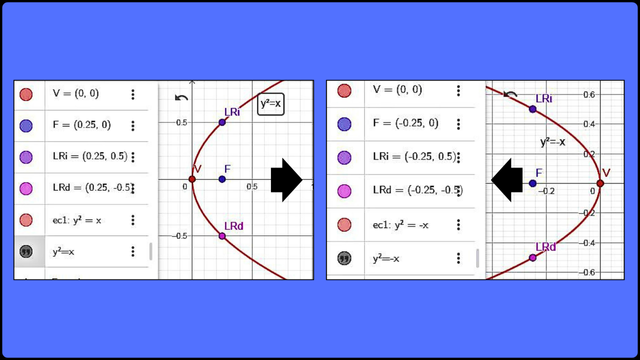_{Representación gráficas de las parábolas con vértice en el origen abriendo a la derecha y a la izquierda F
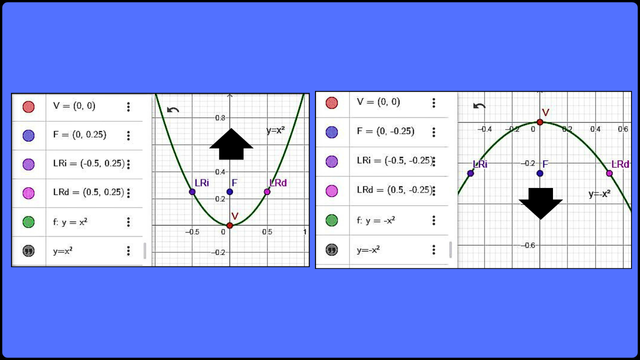Representación gráficas de las parábolas con vértice en el origen abriendo hacia arriba y hacia abajo F}
En estas gráficas podemos apreciar las diferentes posiciones de la parábola con vértice en el origen V(0,0) según la orientación particular del eje de simetría y la posición del punto focal (F) basadas en las ecuaciones canónicas señaladas previamente.

b) Distancia focal del paraboloide
Como lo señalé anteriormente la distancia focal (p) es la distancia que hay desde el vértice (V) al foco (F).

Para el caso de y = 0,1x², determinaremos la distancia focal (p) considerando la ecuación canónica: x² = 4py para lo cual realizamos la siguiente relación:

y = 0,1x² por tanto si despejamos
x² = 10y
x² = 4py

Igualamos ambas ecuaciones, simplificamos y tenemos:

4py = 10y
p = 10/4 = 2.50 ✔

Por tanto, la distancia focal es p = 2.50 metros ✔

c) Ecuación de la directriz
Como lo señalé previamente la directriz es una línea perpendicular al eje de simetría ubicada fuera de la parábola a una distancia (p) desde vértice (V) o 2p desde el punto focal (F).

Para el caso particular de la ecuación y = 0,1x² la directriz es una línea paralela a la abscisa a una distancia p del vértice V(0,0). Por lo tanto, la directriz viene dada por la ecuación lineal:

y = k-p, donde “k” es la ordenada del vértice y “p” la distancia focal.

Siendo el vértice V(0,0), entonces k = 0 y p = 2.50 calculado anteriormente, tenemos que:

y = -2.50. Es la ecuación de la directriz. ✔

_{Distancia focal (p) y línea de la directriz (D) de la parábola y = 0,1x² F}

Escenario número 2.

Es necesario suponer que hay una pelota que se lanza en dirección hacia arriba desde el suelo con una velocidad inicial de 50 pies/s. Supongamos que si la altura de la pelota sobre el suelo viene dada por la ecuación h(t) = -16t² + 50t y aquí t es el tiempo de presentación en segundos entonces;

a) Es necesario representar gráficamente esta ecuación.
b) Averiguar la altura máxima alcanzada por la pelota.
c) Averiguar el tiempo que tarda la pelota en llegar al suelo.

a) Gráfico de la ecuación.
La ecuación h(t) = -16t² + 50t es una parábola cuya función determina la altura (h) alcanzada por la pelota en el tiempo (t) cuando ésta es lanzada hacia arriba desde el suelo con una velocidad inicial de 50 pies/s.

Se pueden determinar puntos claves de la ecuación que nos permitan representar su gráfica en un plano cartesiano (x,y) como los puntos de corte en las abscisas (raíces), el vértice o extremo y el punto de corte en la ordenada.

En este caso, sabemos que la altura de la pelota es cero en el punto de lanzamiento y el punto de llegada al suelo, por tanto podemos determinar dos puntos claves en la ecuación como sigue:

h(t) = -16t² + 50t = 0
-16t² + 50t = 0
(t)(-16t + 50) = 0

Por tanto: t =0 y (-16t + 50) =0
16t = 50
t = 50/16=25/8 = 3.125 segundos.

Por tanto el tiempo total de la trayectoria es 3.125 segundos.✔

De allí obtenemos 2 puntos sobre las abscisas:
T₁ = (0,0) y T₂ = (3.125,0)✔

El vértice V(h,k) o extremo es el punto máximo o mínimo de la parábola donde la pendiente de la curva es igual a cero. Se obtiene a través de la derivada de la ecuación igualando a cero como sigue:

(-16)(2)t + 50 =0
-32t +50 =0
t = 50/32 = 1.5625 segundos

Por tanto, sustituimos este valor en la ecuación:

h(1.5625) = -16(1.5625)² + 50(1.5625)
h(1.5625) = 39.0625 pies ✔

Por tanto, el vértice de la ecuación es el punto V(1.5625,39.0625) ✔

En este caso no existe punto de corte en la ordenada porque la curva pasa por el origen.

En resumen obtuvimos los siguientes puntos claves:
✔ T₁(0,0)
✔ T₂(3.125,0)
✔ V(1.5625,39.0625)

Por tanto, se puede trazar la gráfica de la ecuación h(t) = -16t² + 50t como sigue:

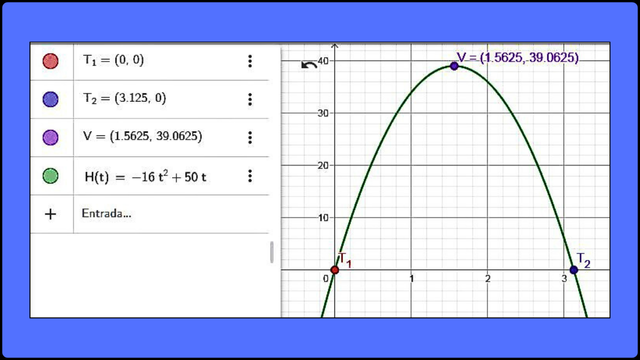_{Representación gráfica de la ecuación h(t) = -16t² + 50t F}
b) Altura máxima alcanzada por la pelota. La altura máxima alcanzada por la pelota se puede determinar con el vértice de la parábola que en este caso, es el punto máximo de la trayectoria o a través del punto medio de la trayectoria total.

Como lo hice previamente calculamos el vértice a través de la expresión deducida de la derivada de la ecuación h(t) = -16t² + 50t, es decir:

(-16)(2)t + 50 =0, despejando t = 50/32 = 1.5625 segundos.✔

Por tanto, la altura máxima se encuentra cuando t= 1.5625, sustituyendo este valor en la ecuación tenemos:

h(1.5625) = -16(1.5625)² + 50(1.5625)
h(1.5625) = 39.0625 pies ✔

Por tanto, el vértice V(1.5625,39.0625) se puede ver representado en el gráfico anterior.

Respuesta.
La altura máxima alcanzada por la pelota es 39.06 pies.✔

c) Tiempo que tarda en llegar al suelo.
En este tipo de movimiento vertical el tiempo de subida y el tiempo de bajada son iguales. Por tanto, ya que conocemos el tiempo para llegar a la altura máxima t_max = 1.5625, el tiempo total (Tt) en llegar al suelo desde su lanzamiento es:

Tt =2t_max = (2)(1.5625)

Tt = 3.125 segundos ✔

También se determinó anteriormente cuando obtuvimos las raíces de la ecuación para h=0, representado en el punto T₂ = (3.125,0) ✔

Respuesta.
El tiempo que tarda la pelota en llegar al suelo desde su lanzamiento es 3.125 segundos


Saludos a @khursheedanwar

Notas:

📌 Imágenes presentadas con la aplicación canva.com
📌 Invito a participar a mis amigos @ridwant @patjewell @paholags @marito74 @genomil @cruzamilcar63 @dasudi @dove11 @goodybest
📌 Más información del concurso en el siguiente enlace.
📌 Mi twitter: steemit_casv

¡Gracias por su visita!