20-02-2025 - Education - Linear Algebra - Vector Product [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

[ENGLISH]
20-02-2025 - Education - Linear Algebra - Vector Product [EN]-[IT]
With this post I would like to provide some brief notions about the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry or linear algebra
(code notes: MOD-64)

Vector Product
To perform a product between two vectors in space we must perform 3 steps: The definition of the vectors, remember the formula of the vector product and finally perform the calculation of the components.

general concept
If we define vectors as follows:

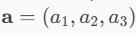
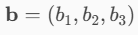
We know that the formula for the vector product is as follows

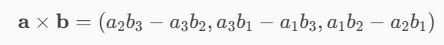
So at this point we need to know how to calculate the X, Y and Z components.
The formulas for calculating the 3 components are shown below

The x component of the vector product is given by
a2b3 - a3b2

The y component of the vector product is given by
a3b1 - a1b3

The z component of the vector product is given by
a1b2 - a2b1

Exercise
Let's try to perform the following exercise related to a vector product

What is the value of the vector product t(2 -3 1) × t(1 0 3) in space?

This exercise is done in 3 steps
1
Definition of vectors
First of all we need to define the vectors we are examining. From the data received we can obtain the vectors.
We will call the vectors a and b
The vector a is:

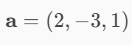
The vector a b:

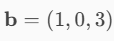
2
Vector product formula
Let's think about a

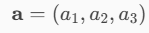
And let's think about b like this:

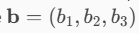
The formula for the vector product written in general form is the following

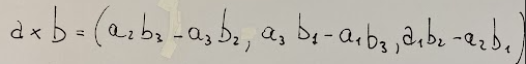
3
Final calculation
Now let's apply the formula described above to the vectors that were given to us and let's do the vector product.

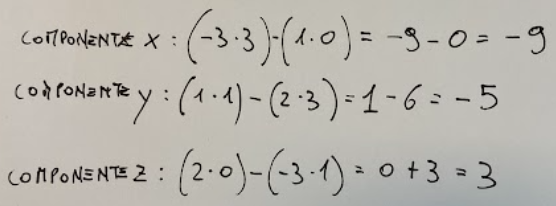
In conclusion we will have that the vector product will be the following

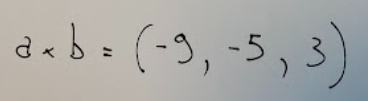
Result
The vector product of

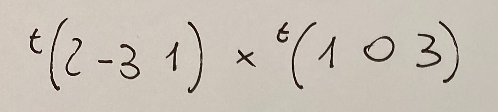
gives as a result

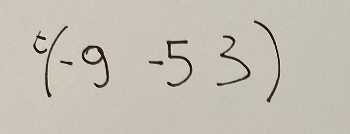
Conclusions
In conclusion, the vector product of two vectors in three-dimensional space is a vector that is perpendicular to both original vectors.

Question
Did you know that the product of vectors in space are calculations widely used in computer graphics?

---

---

[ITALIAN]
20-02-2025 - Education - Algebra lineare - Prodotto vettoriale [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica o algebra lineare
(code notes: MOD-64)

Prodotto vettoriale
Per eseguire un prodotto tra due vettori nello spazio dobbiamo eseguire 3 passaggi: La definizione dei vettori, ricordare la formula del prodotto vettoriale ed infine eseguire il calcolo delle componenti.

concetto generale
Se definiamo i vettori come segue:

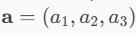
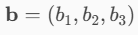
Sappiamo che la formula del prodotto vettoriale è la seguente

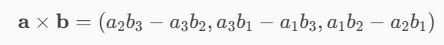
Quindi a questo punto dobbiamo sapere come si calcolano la componente X, Y e Z.
Qui di seguito sono mostrate le formule per il calcolo delle 3 componenti

La componente x del prodotto vettoriale è data da
a2b3 - a3b2

La componente y del prodotto vettoriale è data da
a3b1 - a1b3

La componente z del prodotto vettoriale è data da
a1b2 - a2b1

Esercizio
Proviamo ad eseguire il seguente esercizio relativo ad un prodotto vettoriale

Quanto vale il prodotto vettoriale t(2 -3 1) × t(1 0 3) nello spazio?

Questo esercizio si svolge in 3 passaggi
1
Definizione dei vettori
Prima di tutto dobbiamo definire i vettori che stiamo esaminando. Dai dati ricevuti possiamo ricavare i vettori.
Chiameremo i vettori a e b
Il vettore a è:

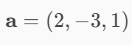
Il vettore a b:

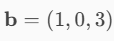
2
Formula del prodotto vettoriale
Pensiamo ad a

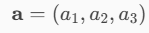
e pensiamo a b così:

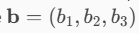
La formula del prodotto vettoriale scritta con in forma generale è la seguente

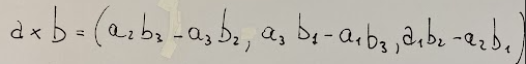
3
Calcolo finale
Andiamo ora ad applicare la formula descritta sopra ai vettori che ci sono stati dati ed andiamo a fare il prodotto vettoriale.

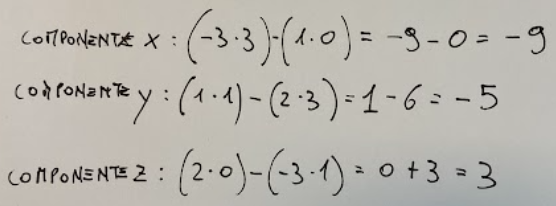
In conclusione avremo che il prodotto vettoriale sarà il seguente

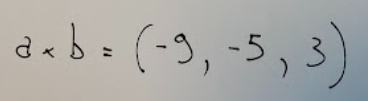
Risultato
Il prodotto vettoriale di

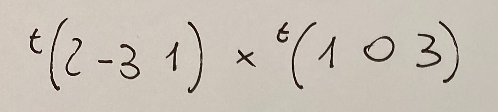
da come risultato

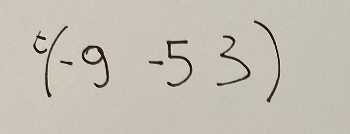
Conclusioni
In conclusione il prodotto vettoriali di due vettori nello spazio tridimensionale è un vettore che è perpendicolare a entrambi i vettori originali.

Domanda
Sapevate che il prodotto di vettori nello spazio sono calcoli molto usati nella computer grafica?

THE END