21-10-2024 - Education - Geometry - basis of a vector space [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

[ENGLISH]
21-10-2024 - Education - Geometry - basis of a vector space [EN]-[IT]
With this post I would like to provide some brief notions about the technical topic mentioned in the subject.
The context in which we operate is that of energy machines.
(code notes: MOD-91)

Basis of a vector space
The basis of a vector space is a set of vectors that have two main characteristics. The two characteristics are linear independence and generation.
**linear independence **
The basis vectors are linearly independent of each other.
This means that none of the basis vectors can be a linear combination of the others.
*generation (also called spanning)
The basis vectors generate the entire vector space, that is, each vector in the space can be written as a linear combination of the basis vectors.
We can express this in the following way:

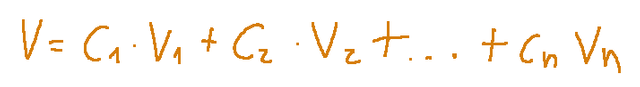
Where:
C1, C2, Cn = scalars

Example:
Let's try to find a basis of every vector space of K<=[x] with m contained in N
Let's try to write the coordinates of the following polynomial:

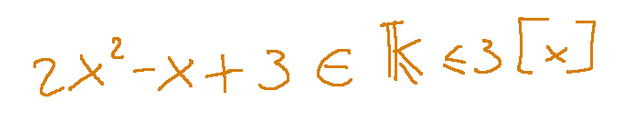
First of all we can say that a basis of

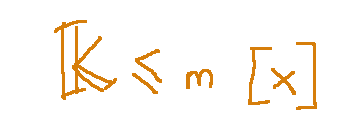
is

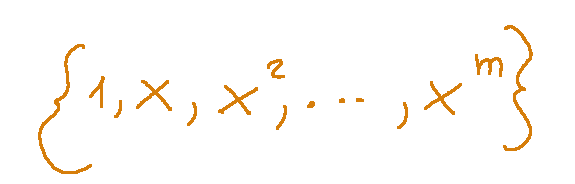
These polynomials generate K=<[x] and are linearly independent.

At this point we take up our expression again

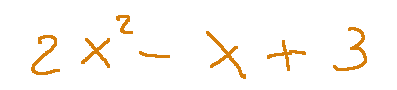
The coordinates are 3, -1, 2

Here are two steps to clarify the concept:

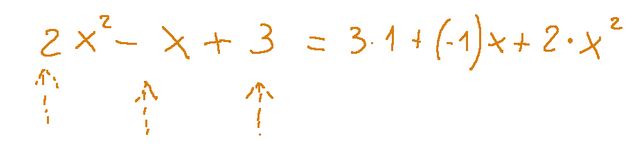
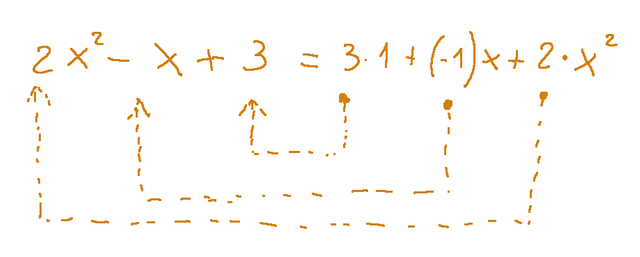
Another example
Take the following ordered set of vectors.

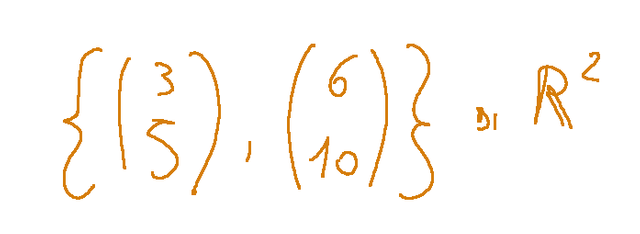
Is this a basis of the respective vector space?
No, because the vectors are not linearly independent. The second vector can be obtained by putting the coefficient 2 to the first vector.

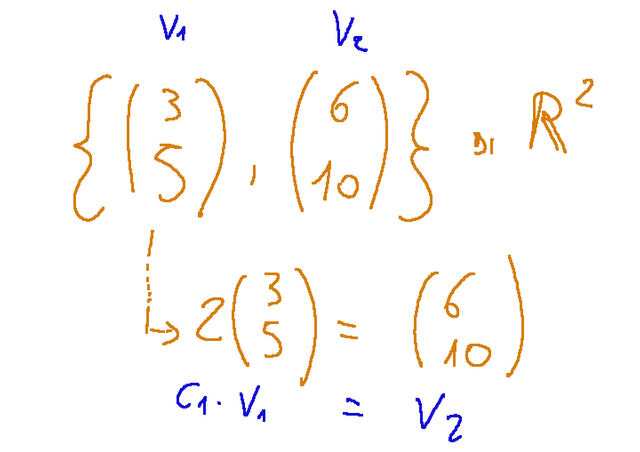
Conclusions
We can conclude by saying that a basis is a set of vectors that allows you to uniquely represent each vector of the vector space as a linear combination of the vectors of the basis.

Question
When you were at school, did you ever do exercises in which you had to find the basis of a vector space?

---

---

[ITALIAN]
21-10-2024 - Education - Geometria - base di uno spazio vettoriale [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello delle macchine energetiche.
(code notes: MOD-91)

Base di uno spazio vettoriale
La base di uno spazio vettoriale è un insieme di vettori che hanno due caratteristiche principali. Le due caratteristiche sono l'indipendenza lineare e la generazione.
**indipendenza lineare **
I vettori della base sono tra di loro linearmente indipendenti.
Questo significa che nessuno dei vettori base può essere una combinazione lineare degli altri.
*generazione (oppure anche chiamato spanning)
I vettori della base generano tutto lo spazio vettoriale, ovvero ogni vettore nello spazio può essere scritto come una combinazione lineare dei vettori della base.
Possiamo esprime questo nella seguente maniera:

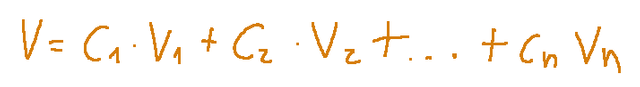
Dove:
C1, C2, Cn = scalari

Esempio:
Proviamo a trovare una base di ogni spazio vettoriale di K<=[x] con m contenuto in N
Proviamo a scrivere le coordinate del seguente polinomio:

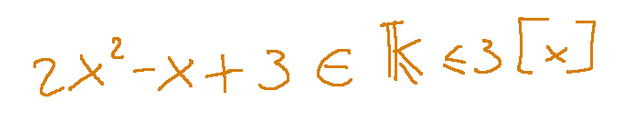
Innanzitutto possiamo dire che una base di

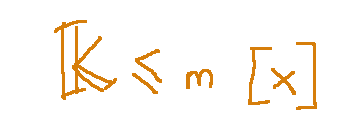
è

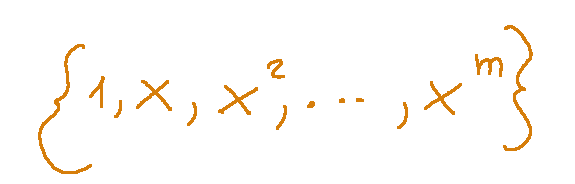
Questi polinomi generano K=<[x] e sono linearmente indipendenti.

A questo punto riprendiamo in mano la nostra espressione

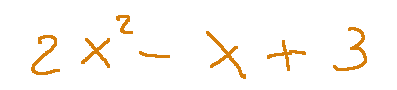
Le coordinate sono 3, -1, 2

Qui di seguito due passaggi per chiarire il concetto:

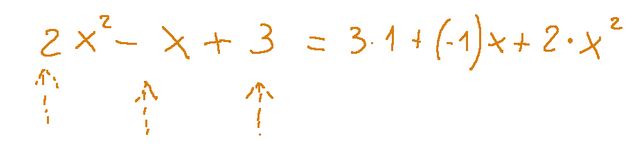
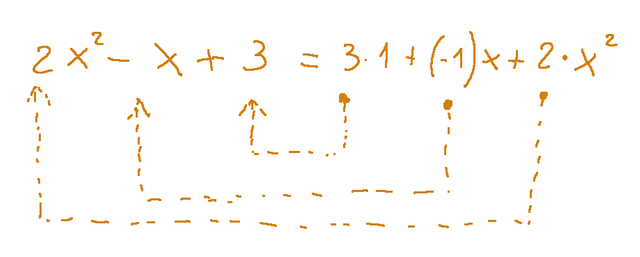
Altro esempio
Prendiamo il seguente insieme ordinato di vettori.

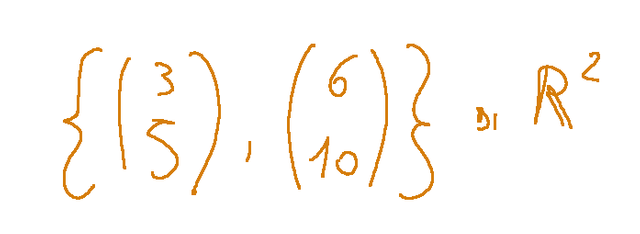
Questo è una base del rispettivo spazio vettoriale?
No, perché i vettori non sono linearmente indipendenti. Il secondo vettore è ottenibile mettendo il coefficiente 2 al primo vettore.

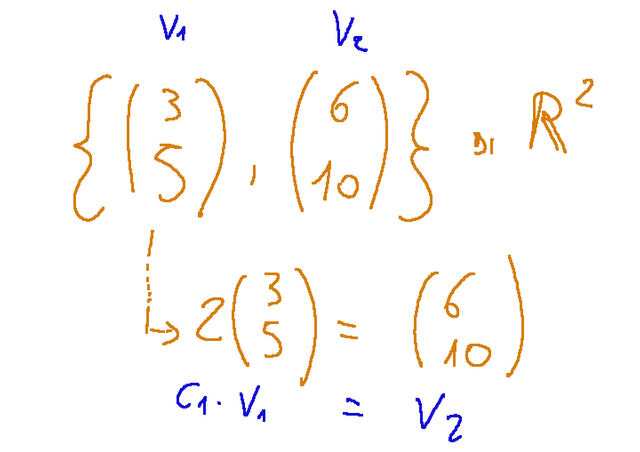
Conclusioni
Possiamo concludere dicendo che una base è un insieme di vettori che permette di rappresentare in modo univoco ogni vettore dello spazio vettoriale come combinazione lineare dei vettori della base.

Domanda
Quando andavate a scuola avete mai fatto esercizi in cui dovevate trovare la base di uno spazio vettoriale?

THE END