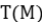
MÓDULOS DE TORSIÓN
Consideremos un dominio de integridad A y M un módulo sobre A. Se define la torsión T(M)={ m ∈M: existe r∈A, r ≠0 tal que rm=0} . Es fácil ver que T(M) es un submódulo de M. Si T(M)=0, se dice que el módulo es sin torsión y si T(M)=M se dice que M es de torsión.
Veamos que T(M/T(M))=0.
En efecto , si r(m+T(M))=0, con r ≠0, luego rm ∈ T(M), luego existe s≠0 con (rs)m=0 y como rs≠0, se deduce que m∈T(M), es decir m+T(M)=0, lo que prueba lo afirmado.
Si f:M → N es un morfismo de módulos sobre A, entonces f(T(M))⊂T(N),
En efecto, si m ∈T(M), existe r ≠0 con rm=0, luego f(rm)=rf(m)=0, lo que dice que f(m) ∈T(N).
Si
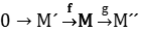
entonces es exacta
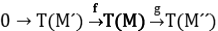
Sólo hay que demostrar que Ker(g|T(M))⊂f(T(M´). En efecto, sea m ∈ Ker(g|T(M)), luego existe m´ ∈M´con f(m´)=m y como existe r ≠0 con rm=0, luego f(rm´)=0, es decir rm´=0 y por lo tanto m´ ∈ T(M´).
Si k es el cuerpo cociente del dominio A y f:M → k⊗AM, definido por f(m)=1⊗m, entonce Kerf=T(M).
Recuerdo que si S ⊂ A es un conjunto multiplicativo con 0 ∉ S, y AS es el anillo localizado, entonces AS⊗AM ≅ MS (r/s ⊗m → m/s). Si consideramos S=A*= {r ∈ A: r ≠0 }, entonces K= AS. Por lo tanto k⊗AM =AA*⊗AM ) ≅ MA*. Si f(m)=1⊗m=0, luego m/1=0. Existe un s ∈ A* con sm=0, Es decir m ∈ T(M). Recíprocamente, si m ∈ T(M), entonces sm=0 para algún s∈ A*, luego m /1=0 y por el isomorfismo 1⊗m=0. Esto termina la prueba.
T(MS)=T(M)S
Si m/s ∈ T(MS) existe r≠0, tal que r( m/s)=0, luego existe s ∈S tal que s(rm)=0 y como sr ≠0 se deduce que m ∈ T(M), es decir m/s ∈ T(M)S. Por otro lado, si m/s ∈ T(M)S, entonces existe r≠0 con rm=0, luego r(m/s)=0, es decir m/s ∈ T(MS). Esto termina la prueba.
Terminamos con el siguiente resultado:
Son equivalentes: (a) M es sin torsión (b) MP es sin torsión para todo ideal primo P (c) MP es sin torsión para todo ideal máximal P .
Si vale (a), sabemos que T(MP)=T(M)P=0, esto dice que vale (b).
Si vale (b) es claro que vale (c)
Finalmente si vale (c), T(M)P=0, para todo ideal máximal P de A, luego T(M)=0.
NOTA
Es importante referir que lo desarrollado en estas notas son soluciones a los ejercicios de torsión del capítulo 3 del libro de M.F. Atiyay, y I. G Macdonal: Introducción al Algebra Conmutativa. Editorial Reverte. 1978.
You've got a free upvote from witness fuli.
Peace & Love!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit