Students come home needing help with their trig homework. This article will give a simple definition of how trig ratios work.
Students have always needed help with their homework. The most troublesome area for most students is mathematics. Generally by the time students have reached classes beyond general math parents have stopped trying to help them. The six trigonometric functions are very easy to find once the basics are understood.
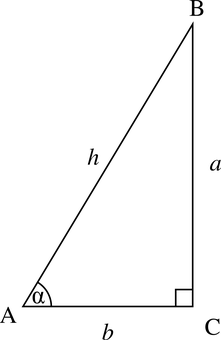
The Background
Trigonometric functions are found based on right triangles. A right triangle is a triangle which has one angle exactly 90 degrees. The other two angles would be less than 90 degrees because total degrees in a triangle is 180. One of the angles is designated as θ or "theta" and is the angle which will be used to find the trig functions. When θ is written in trig functions it is the angle measure we are using.
The triangle has three sides. The side opposite the right angle is called the hypotenuse and is usually the longest side on the triangle. The naming of the other two sides for trig functions depends on which angle we are using as θ. The side closest to θ is called adjacent because it is right next to θ. The other side is called opposite and is the one farthest from θ. These sides are used in ratios to find the trigonometric functions.
The Three Basic Functions
Sine is the first of the three basic functions. Sine is found by dividing the length of the opposite side by the length of the hypotenuse. In books it is generally written as sin θ.
Cosine is the next of the three basic functions. Cosine is found by dividing the length of the adjacent side by the length of the hypotenuse. In books it is generally written as cos θ.
Tangent is the final of the three basic functions. Tangent is found by dividing the length of the opposite side by the length of the adjacent side. In books it is generally written as tan θ.
An easy way to remember which side goes with sine and which side goes with cosine is to think of close. Close and cosine sound similar. Cosine uses the adjacent side which is the closer side.
The Reciprocal Functions
Each of the three basic functions has a reciprocal function. A reciprocal function is the ratio turned upside down. The three reciprocal functions are cosecant, secant and cotangent.
Cosecant is the reciprocal of sine. It is found by dividing the length of the hypotenuse by the length of the opposite side. It is usually written as csc θ in books.
Secant is the reciprocal of cosine. It is found by dividing the length of the hypotenuse by the length of the adjacent side. It is usually written as sec θ in books.
Cotangent is the reciprocal of tangent. It is found by dividing the length of the adjacent side by the length of the opposite side. It is usually written as cot θ in books.
Using a calculator will give a student a decimal approximation of the each of the functions. Using simply the values of the sides will give the student an exact measure. If two of the side measures are given the Pythagorean formula can be used to find the third.
References:
Algebra & Trigonometry Second Edition by Robert Blitzer, Prentice Hall Publishing