I think you can use induction to the number of vertices. Let G be a graph with only 1 vertex. To satisfy the condition "e is not less than v", it must have a loop. So, G has a cycle.
Now suppose that the statement is true for all graphs with number of vertices at most k. Consider a graph G with (k+1) vertices and suppose that |E(G)| is not less than |V(G)|. If G has no cycles, than it must have a "leaf", v_0. (A leaf means a vertex of a graph of degree 1.)
Now consider the graph H we get by removing the vertex v_0 from G. Then H is a graph with k=|V(G)|-1 vertices and |E(G)|-1 edges. So, the number of edges of H is not less than the number of vertices of H. By the induction hypothesis, H must contain a cycle. However, since H is a subgraph of an acyclic graph G, H cannot contain a cycle. This is a contradiction.
Now we see that the statement holds for all graphs with finite number of vertices.
RE: Ran Across An Interesting Math Problem - Can You Solve It?
You are viewing a single comment's thread from:
Ran Across An Interesting Math Problem - Can You Solve It?
For the proof of the theorem that an acyclic graph with finite vertices must have a leaf, see the article "Acyclic graph must have a leaf" on math.stackexchange.com
There is a reply that shows a "tree(connected, acyclic graph)" with finite vertices has a leaf. One can easily generalize this theorem and prove that a "forest(acyclic graph)" with finite vertices must have a leaf.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Will do, thanks. I'm checking the proof right now. Thanks for the response.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I was just going over proofs on StackExchange and I think you're correct. I would be very impressed if you found this organically by yourself, but still since you answered it right I owe you 3 SD. I'll send that to you when I have that amount.

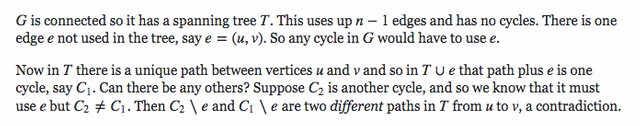

Here are some examples of the proof I found:
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit