The "golden ratio" (φ) can be understood as a scale-factor that increases the scale of anything with everything that came before, approximated in the Fibonacci series Fn + Fn-1 = Fn+1, 3, 5, 8, 13, 21, 34, 55, and so on, a universe of state n grows by its current state plus its previous state that is also all that preceded it, a bit slower an exponential curve than doublings (φ^n rather than 2^n).
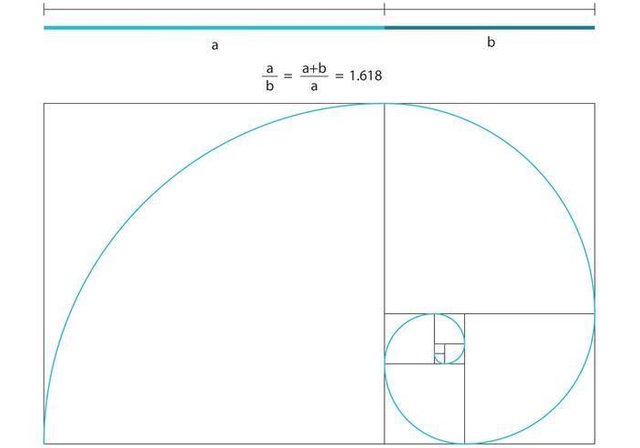
The configuration of microtubules follows base-φ to some extent, as in are multiples of φ and divisible by φ. The microtubules are 13 tubulin filaments in circumference, a Fibonacci number, and tubulin dimers overall follow a 5-step (approximated as 13/φ^2) and 8-step repetition (approximated as 13/φ), as well as a 13-step repetition that is the tubulin filament itself.
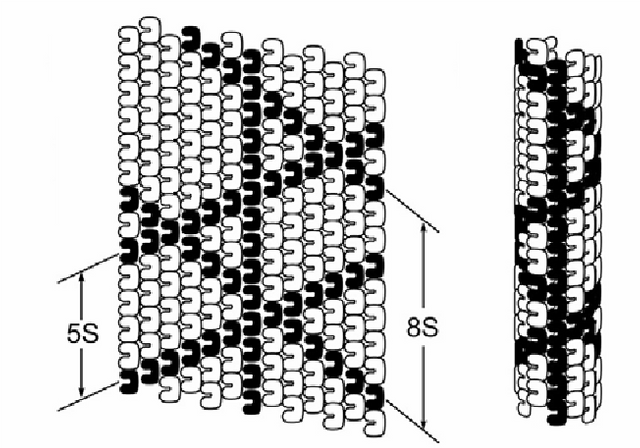
The 7-tubulin memory "bytes", 6 bit with a central "address dimer", also follow a 5-step repetition, with a 3 + 2 + 3 + 3 + 2 = 13 arrangement along the circumference, as well as an 8-step repetition, all Fibonacci numbers.
oh now i get it this can be used for a better implementation in this
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit