INTRODUCCIÓN
En esta oportunidad desarrollaremos aplicaciones prácticas con ayuda de la herramienta computacional NONLIN V 7.14, teniendo como orientación los aspectos cualitativos que se dedujeran de los desarrollos matemáticos desde un enfoque energético hechos a cada uno de los términos integrantes de la ecuación diferencial de equilibrio dinámico en la parte I de este trabajo, por lo que es importante querido lector, que tengas muy presente las ideas allí disertadas, para que te disfrutes al máximo la continuación de dicho trabajo. Una de las ideas más importantes que vale la pena traer a colación y basados en la ecuación N°01, es la concerniente al hecho de que la energía asociada al amortiguador viscoso “Ed” crece en una relación directa proporcional con el consecuente incremento de los valores de la frecuencia de la excitación externa “ω”, deformación dinámica máxima “uo” y fracción de amortiguamiento crítica “ξ”, hecho que se puede inferir de manera cualitativa en la ecuación N°01; dado que la frecuencia natural “ωn” está conectada con la rigidez “K”, no consideramos el incremento del valor de esta propiedad en el aumento de “Ed”, porque si “K” aumenta “ωn” también, y este último término está en el denominador.
Ahora bien, una de las limitantes de la ecuación N°01 es que no incluye la variable tiempo; si bien “uo” por tratarse de una excitación armónica y un régimen de vibración estacionario es el mismo en cada ciclo de vibración, es necesario en nuestros razonamientos tener presente que en cada ciclo (ver imagen N°01) la masa volverá a su posición original, pero en ese proceso se produce un balance energético, cuya variable tiempo es trascendental tomarla en cuenta; es por ello, que le damos la bienvenida al uso de la herramienta computacional NONLIN V 7.14.
Imagen N°01: una visión global de los contenidos a estudiar
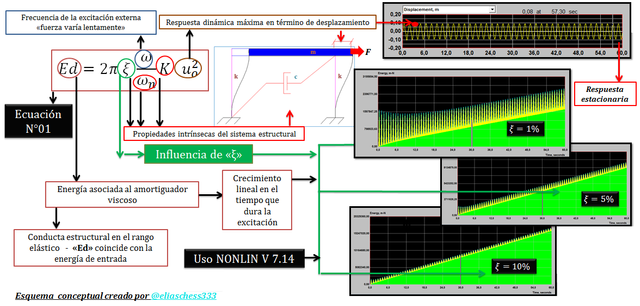
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El pórtico fue elaborado con el programa AutoCAD 2010. Los gráficos resaltados en color negro, provienen de la herramienta computacional NONLIN V 7.14.
Apreciamos en la imagen N°01 una serie de gráficos obtenidos por dicha herramienta computacional, que sustentan el planteamiento de la siguiente interrogante, eje central de este trabajo:
¿A qué se debe que “Ed” aumente linealmente en el tiempo?
También estos gráficos, permiten ver desde un enfoque energético, el protagonismo que cobra el amortiguamiento en el balance energético, en la medida que “ξ” aumenta, por lo que en función de esta propiedad hemos definido una serie de casos de estudios, lo cuales se detallan de mejor manera en el tópico concerniente a “DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR”. Es importante, que tengas amigo lector, ciertas nociones básicas de la dinámica estructural para una adecuada comprensión de este trabajo, por lo que te sugiero la revisión de las referencias N°04 y N°05.
DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR
El modelo estructural con el que estaremos desarrollando las aplicaciones prácticas con la intención de hacer didáctica la presentación de las ideas, presenta las mismas propiedades que el utilizado en la parte I de este trabajo (ver referencia N°03), consistente en líneas generales en un pórtico plano de un grado de libertad tanto estático (asociado al posible desplazamiento de la junta) como dinámico (asociado al movimiento de la masa), debido a que nos fundamentamos en la hipótesis de concebir a los elementos verticales indeformables axialmente (área infinita) y al elemento horizontal como un cuerpo rígido (área infinita e inercia infinita); además la conducta de este pórtico ante excitaciones externas se da en el rango elástico, es decir, no ocurre degradación de la rigidez, puesto que es el amortiguador viscoso el encargado de disipar la energía de entrada. En este sentido es necesario establecer los valores de las propiedades intrínsecas de la estructura, que estratégicamente he resaltado en líneas anteriores, centrando en la propiedad relativa al amortiguamiento el surgimiento de los diversos casos de estudios que estaremos simulando en la herramienta computacional NONLIN V 7.14:
Imagen N°02: casos de estudios, asociados a la variación de “ξ”
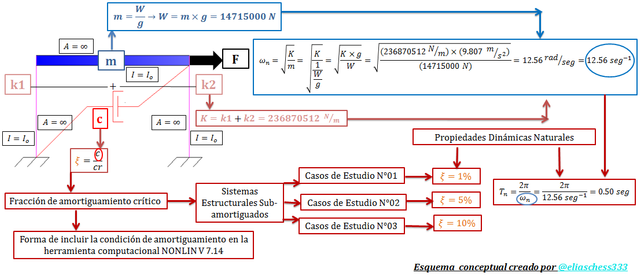
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El pórtico fue elaborado con el programa AutoCAD 2010.
De acuerdo a lo observado en la imagen N°02, los casos de estudio van a estar en función de variar los valores de la fracción de amortiguamiento crítico “ξ”; es importante en este punto que revises la referencia N°04, para que afiances las nociones acerca el amortiguador viscoso “c”, y así comprendas como en las aplicaciones prácticas el dato que típicamente utilizamos es “ξ”; cuyo valor en las estructuras de interés en el campo de la ingeniería sismoresistente, tales como edificios, represas, puentes, entre otras, es menor al 10%, de allí a que este sea el tope fijado en los casos de estudio. Por su parte el período natural “Tn”, será el mismo en todos los casos. Establecidas las propiedades dinámicas de la estructura, procedamos ahora a tratar la fuerza externa “F”, consistente en una excitación armónica.
Imagen N°03: definiendo los parámetros de la excitación externa
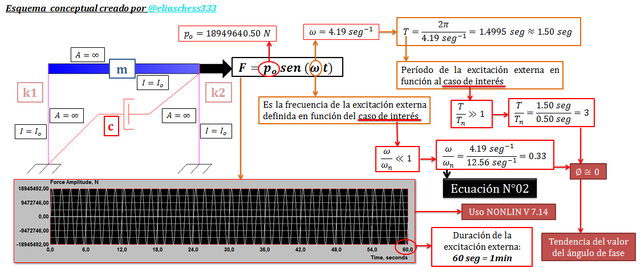
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El pórtico fue elaborado con el programa AutoCAD 2010. El gráfico resaltado en color rojo, proviene de la herramienta computacional NONLIN V 7.14.
Para este caso de relación de frecuencias o períodos, Chopra (2014) indica que el ángulo de fase “ϕ” tiende a un valor de cero, lo cual está en sintonía con los tratamientos matemáticos desarrollados en la parte I de este trabajo, en el cual se dedujo una expresión que permite también sustentar el valor al cual tiende “ϕ”; la misma se presenta a continuación:
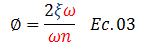
Evaluamos esta ecuación con los valores característicos del problema en estudio, acotando que el cálculo del cociente resaltado en color “rojo” se ilustra en la imagen N°03 (ver Ec. 02), y el valor de “ξ”, corresponde al caso de estudio N°03, por ser el mayor valor:
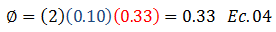
La tendencia de “ϕ” a cero se agudiza, en la medida que disminuimos el valor de “ξ”. Finalmente es importante señalar que en el proceso de simulación en el NONLIN V 7.14, estableceremos arbitrariamente como tiempo de duración de la excitación externa, un minuto.
EXPLICACIÓN DEL PROCESO TÍPICO DE LA INCLUSIÓN DE LOS DATOS EN EL PROGRAMA NONLIN V 7.14
Basado en lo expuesto en párrafos anteriores, estamos preparados para definir todas las condiciones que nos permitirán simular el modelo estructural en el programa NONLIN V 7.14. Comencemos con la introducción de los datos que se ilustran en el esquema conceptual de la imagen N°02:
Imagen N°04: estableciendo las propiedades dinámicas naturales de la estructura en estudio
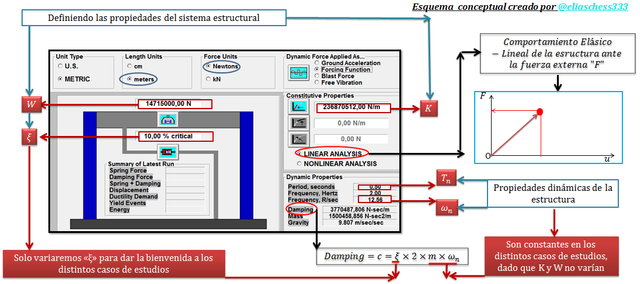
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. La imagen resaltada en el recuadro negro, proviene de la herramienta computacional NONLIN V 7.14.
Tal como se señala en la imagen N°04, para poder simular los distintos casos de estudios, sólo estaremos modificando el parámetro concerniente a la fracción de amortiguamiento crítico “ξ”. En lo que respecta a la definición de “F” en el programa NONLIN V 7.14, nos basamos en los aspectos que se definieron en el esquema conceptual de la imagen N°03.
Imagen N°05: establecimiento de parámetros de la excitación externa
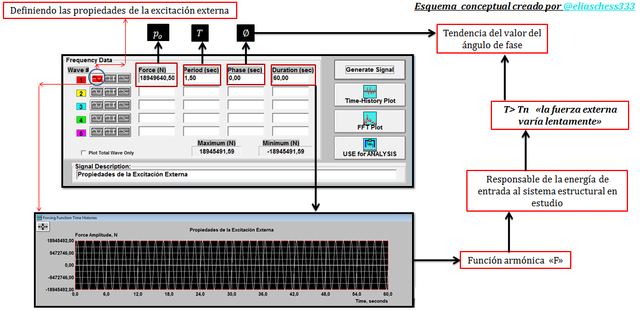
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. Las imágenes resaltadas en el recuadro negro, provienen de la herramienta computacional NONLIN V 7.14.
Una vez incluida esta información en el programa NONLIN V 7.14, estamos listos para correr el modelo. En consonancia con la delimitación de la temática a estudiar, de la información que proporciona el programa, nos centraremos en los gráficos que nos permiten visualizar el balance energético que se da entre las propiedades intrínsecas de la estructura, como lo son su masa “energía cinética-Ek”, rigidez “energía potencial-Es” y amortiguamiento “energía asociada al amortiguador viscoso-Ed”.
INTERPRETACIÓN DE RESULTADOS ARROJADOS POR LA HERRAMIENTA COMPUTACIONAL NONLIN V 7.14
En los esquemas conceptuales de las imágenes N°06, N°07 y N°08, apreciamos como característica común, un crecimiento lineal de la energía asociada al amortiguador viscoso “Ed”, mientras que la energía potencial y la cinética no experimentan cambios en el tiempo, aspecto que se demostró en la parte I de este trabajo.
Imagen N°06: caso de estudio N°01, ξ=1%
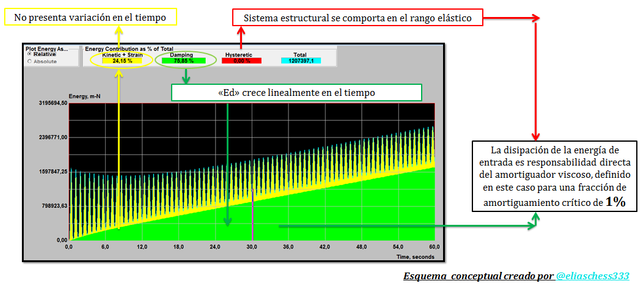
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El gráfico resaltado en color negro, proviene de la herramienta computacional NONLIN V 7.14.
Imagen N°07: caso de estudio N°02, ξ=5%
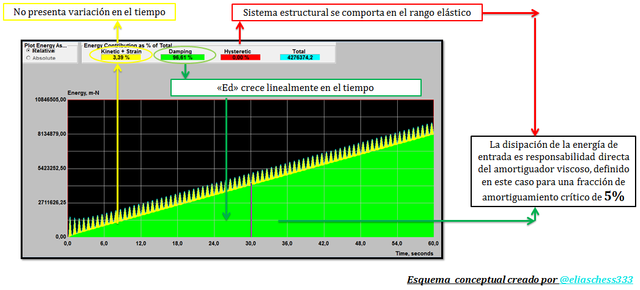
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El gráfico resaltado en color negro, proviene de la herramienta computacional NONLIN V 7.14.
Imagen N°08: caso de estudio N°03, ξ=10%
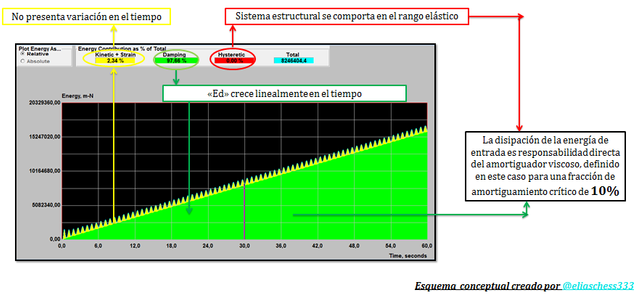
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El gráfico resaltado en color negro, proviene de la herramienta computacional NONLIN V 7.14.
Ahora bien, para dar respuesta a la interrogante planteada al inicio de este trabajo, he decidido preparar el siguiente recurso audio visual, donde explico de un modo didáctico, nociones generales que nos permiten comprender este fenómeno:
▶️ DTube
▶️ IPFS
Fuente: @eliaschess333, año: 2018. Nota: video elaborado por el autor con ayuda de las herramientas computacionales Camtasia Studio 8, Adobe Audition 3.0. Los esquemas conceptuales que se presentan fueron elaborados por el autor con las herramientas Microsoft PowerPoint y Paint. La simulación del modelo estructural fue realizada con el programa NONLIN V 7.14.
Adicionalmente es importante señalar, que en la medida que aumentamos los valores de fracción de amortiguamiento crítico “ξ”, el componente energético asociado a la rigidez y a la masa tiende a disminuir (franja de color “amarillo” en los gráficos de las imágenes N°06, N°07 y N°08), lo cual es totalmente lógico. Si el valor de “ξ” lo aumentamos, hasta llegar a cien por ciento, ocurriría que el sistema no vibraría (sistemas amortiguados), y evidentemente la franja de color “amarillo” desaparecería. No obstante, como se señaló anteriormente, las estructuras de interés en el campo de la ingeniería sismoresistente presentan en la práctica valores de “ξ” menor al diez por ciento, es decir, son sistemas sub-amortiguados que vibran ante excitaciones externas. Presentar gráficos de energía, para distintos valores de “ξ” permite afianzar de un modo alternativo esta propiedad dinámica, complementando, los estudios que hemos realizados en trabajos anteriores.
CONCLUSIONES
Las herramientas computacionales que permiten modelar sistemas estructurales, y su interacción con cargas externas, bien sean de carácter dinámico o estático, sin lugar a dudas que son un excelente aliado para nosotros los amantes de la ingeniería sismoresistente. Una muestra de este hecho, es este trabajo que con mucho gusto y esfuerzo presenté para ustedes queridos lectores, donde las ideas que se dedujeron de la ecuación N°01, fueron contrastadas en el programa NONLIN V 7.14, llegando a las siguientes conclusiones de interés:
1.- En la medida que aumentamos el valor de “ξ” mayor será la energía asociada al amortiguador viscoso; “Ed”.
2.- Se tiene que “Ed” se va incrementando en el tiempo que dura la excitación externa, como una muestra fiel, de la necesitad de disipar la energía de entrada que esta introduce al sistema estructural.
3.- Lo anterior va en consonancia al comportamiento que hemos asumido en este estudio para el pórtico que se analiza, es decir, un comportamiento perfectamente elástico, donde el amortiguador viscoso es el responsable de disipar la energía de entrada.
4.- Esta conclusión N°03 permite argumentar el hecho de que las energías asociadas a los componentes de rigidez y de masa no varíen en el tiempo.
Escribió para ustedes:
FUENTES DE INFORMACIÓN CONSULTADAS
01.- CHOPRA ANIL K. 2014. DINÁMICA DE ESTRUCTURAS. CUARTA EDICIÓN. PEARSON EDUCACIÓN, MÉXICO.
02.- NONLIN “EDUCATIONAL PROGRAM FOR LEARNING THE CONCEPTS OF STRUCTURAL DYNAMICS AND EARTHQUAKE ENGINEERING”. DEVELOPED BY DR. FINLEY CHARNEY, NONLIN IS AVAILABLE AS ONLINE TOOL THROUGH NEESHUB: HTTP://NEES.ORG/
LECTURAS RECOMENDADAS
03.- SANTANA E. 2018. ABORDAJE DIDÁCTICO DEL CONCEPTO DE ENERGÍA DESDE EL ENFOQUE DE LA INGENIERÍA SISMORESISTENTE. CASO: SISTEMAS QUE SE COMPORTAN ELÁSTICAMENTE SOMETIDOS A UNA VIBRACIÓN FORZADA ARMÓNICA. PARTE I. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/abordaje-didactico-del-concepto-de-energia-desde-el-enfoque-de-la-ingenieria-sismoresistente-caso-sistemas-que-se-comportan
04.- SANTANA E. 2018. DETERMINACIÓN EXPERIMENTAL DEL AMORTIGUAMIENTO EN ESTRUCTURAS. UN ENFOQUE MATEMÁTICO CON APLICACIONES EN LA INGENIERÍA SISMORESISTENTE DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/determinacion-experimental-del-amortiguamiento-en-estructuras-un-enfoque-matematico-con-aplicaciones-en-la-ingenieria
05.- SANTANA E. 2018. ESTUDIO DE LAS APLICACIONES DEL ANÁLISIS MATRICIAL EN LA OBTENCIÓN DE LA MATRIZ DE RIGIDEZ DE UN PÓRTICO PLANO. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/estudio-de-las-aplicaciones-del-analisis-matricial-en-la-obtencion-de-la-matriz-de-rigidez-de-un-portico-plano
watch for free tutorials (Autocad-Photoshop-Sketchup-Lumion-Revit)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Estimado @eniolw complacido por las apreciaciones que realizas. Agradecido por el apoyo compañero. Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Buen trabajo @eliaschess333
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias por el apoyo @germanmontero. Saludos compañero!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Excelente trabajo Elias! complejo y a la vez didáctico!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @eliaschess333! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @eliaschess333! You received a personal award!
Click here to view your Board of Honor
Do not miss the last post from @steemitboard:
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @eliaschess333! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board
If you no longer want to receive notifications, reply to this comment with the word
STOPDownvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit