Bien estimada comunidad, ya les he hablado de lo que es un algoritmo, representación de este mediante diagramas y las proposiciones. Ahora me toca hablarles de la tabla de la verdad. Es muy interesante esta parte, porque desde este punto en donde se comenzaran a evaluar las proposiciones, condiciones que permitirán saber cual es verdadera o falsa, y que camino tomar cuando tengamos una respuesta de esta evaluación.
Fuente
¿Qué es la tabla de la verdad?
La tabla de la verdad es uno de los métodos más sencillos y conocidos de la lógica formal, pero la mismo tiempo también uno de los más poderosos y claros. Entender bien las tablas de verdad es, en gran medida, entender bien a la lógica formal misma.
Ahora bien, esta está compuestas de los signos lógicos como: NO, O, Y, SI…ENTONCES, SÍ SÓLO SÍ. No se preocupen, es más sencillo de lo que piensan. Aunque realmente lo importante acá es que entiendan como se combinan las proposiciones y el resultado que arroja cuando se usa con los signos lógicos NO, O e Y (para efectos de programación).
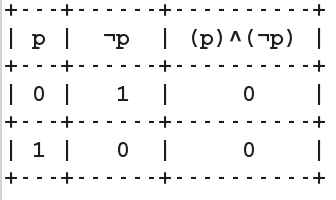
Signo lógico NO (¬)
Este no hace mas que negar la proposición a la que está acompañando. Supongamos la siguiente proposición:
- Las plantas realizan un proceso llamado fotosíntesis.
Al acompañarla del signo lógico ¬, esta cumplirá la función de negar la proposición, quedando de la siguiente manera:
- Las plantas no realizan un proceso llamado fotosíntesis.
Sabemos que al anteponer el signo lógico NO, estamos volviendo falsa una proposición que es verdadera, y aquí es donde entran en juego las proposiciones Y y O, ya que se combinan para dar un resultado lógico con respecto a la vida real.
Signo lógico Y (^)
Se que les parece un poco extraño el símbolo, pero es fácil de memorizar porque es lo inverso a como se escribe la letra que lo representa. Esta se usa para comparar dos o más proposiciones, y el resultado será verdadero cuando ambas sean verdaderas. Veamos el siguiente ejemplo:
(A) El cielo es azul
(B) La luna es un satélite natural
Hacemos la siguiente combinación:
| A | B | A^B | Lectura |
|---|---|---|---|
| V | V | V | El cielo es azul y la luna es un satélite natural |
| V | F | F | El cielo es azul y la luna no es un satélite natural |
| F | V | F | El cielo no es azul y la luna es un satélite natural |
| F | F | F | El cielo no es azul y la luna no es un satélite natural |
Signo lógico O (v)
Hay que tener cuidado con los símbolos, porque es común llegar a confundir el signo lógico de O por el de la Y, por eso recomiendo seguir el consejo de llevarle la inversa a la escritura de la Y (^) para recordar ese detalle. El signo lógico O es muy abierta, solo hace falta que se cumpla una proposición u otra para poder tener un resultado verdadero. Vamos al ejemplo:
(A) Plutón no es un planeta.
(B) El invierno es frío.
| A | B | AvB | Lectura |
|---|---|---|---|
| V | V | V | Plutón no es un planeta o el inverno es frío |
| V | F | V | Plutón no es un planeta o el inverno no es frío |
| F | V | V | Plutón si es un planeta o el inverno es frío |
| F | F | F | Plutón si es un planeta o el inverno no es frío |
Estas formas lógicas son las que se usan en la programación, y son las que están representadas a nivel de código. Poco a poco se los iré detallando. Ahora veamos un ejercicio con la combinación de las tres formas lógicas explicadas.
(A) El cielo es azul
(B) La luna es un satélite natural
(C) Plutón no es un planeta.
| A | B | AvB | ¬(AvB) | ¬(AvB)^C |
|---|---|---|---|---|
| V | V | V | F | F |
| V | F | V | F | F |
| F | V | V | F | F |
| F | F | F | V | F |
Evaluando el resultado del ejercicio anterior
1. La columna tres muestra el resultado al evaluar las proposiciones con el signo lógico O.
2. La columna cuatro revertimos el resultado de la columna tres, debido a que es la negación de la misma.
3. La columna cuatro evalúa la columna tres con la proposición C a través del valor lógico Y, teniendo como resultado todas las combinaciones como falso. A esto se le llama una Contradicción, ya que la última columna de la tabla de verdad está formada únicamente valores falsos. Cuando está completamente llena de valores verdaderos, se le conoce como Tautología.
2. La columna cuatro revertimos el resultado de la columna tres, debido a que es la negación de la misma.
3. La columna cuatro evalúa la columna tres con la proposición C a través del valor lógico Y, teniendo como resultado todas las combinaciones como falso. A esto se le llama una Contradicción, ya que la última columna de la tabla de verdad está formada únicamente valores falsos. Cuando está completamente llena de valores verdaderos, se le conoce como Tautología.
Espero haya sido de su agrado este post, y si les quedó alguna interrogante, no duden en preguntar y dejar sus comentarios. Hasta una nueva oportunidad, se les aprecia mucho.
Saludos.
¡Felicidades, #proconocimiento te valoró!
Has sido reconocido(a) por tu buen post por el Comité de Arbitraje y Valoración del Proyecto Conocimiento @proconocimiento.
Apoyamos y valoramos tu esfuerzo...
Proyecto Conocimiento es parte de la comunidad @provenezuela.
Pioneros en la plataforma #steemit en el reconocimiento y valoración a la Producción Intelectual en habla hispana.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by agustinoro2010 from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit