Hola amigos bienvenidos una vez más a nuestro encuentro matemático. En esta oportunidad, quisiera compartirles un contenido referido a las estructuras algebraicas, de manera particular, hoy les traigo las estructura de monoide y semigrupo. En siguientes publicaciones iremos abordando otras estructuras más complejas hasta que lleguemos a la mayor de ellas, los espacios vectoriales.

---

---

Estructuras Algebraicas

En su forma más simple, una estructura algebraica es un elemento, u objeto, matemático formado por un conjunto no vacío y una relación o Ley de Composición Interna definida en él. En situaciones más complejas podría definirse más de una ley de composición interna en el conjunto e incluso una ley de composición externa. Según sean las propiedades que deban satisfacer dichas leyes de composición, se tienen los distintos tipos de estructuras algebraicas, que no son, en rigor, sistemas axiomáticos.

---

---

Estructura de monoide

El monoide es la estructura algebraica más simple, respecto a ella no existe un definición consensuada, o única, en el mundo del algebra moderna. Sin embargo, adoptaremos una de las más utilizadas la cual no señala lo siguiente:

El par (M, *) donde es distinto de vacío y * es una función, es un monoide si y sólo si * es una ley de composición interna en M

Son ejemplos, o modelos, de monoides los conjuntos de los números naturales (N), enteros (Z), racionales (Q), reales (R) y complejos (C), con la suma ordinaria de números. Fácilmente puedes se apreciar la operación suma (+), es cerrada en cada uno de los conjuntos numéricos antes referidos.

Casos particulares, a modo de ejemplos, de los monoides (N, +) y (Z, +)

---

---

---

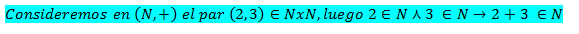
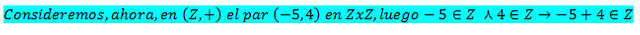
Semigrupo

El par (A.*), donde A es un conjunto distinto de vacío y * es una función, es un semi grupo si y solo si * es un ley interna y asociativa en A.

---

En otras palabras, un semigrupo es un monoide asociativo

Si fuera el caso que un semigrupo verifica la conmutatividad, se dice que el semigrupo es conmutativo y si además tiene elemento neutro el semigrupo tiene unidad. Al elemento neutro suele llamarse identidad.

Es un modelo de semigrupo conmutativo, con unidad el par ( N, +) , puesto que la suma ordinaria en N es asociativa (tres o más números naturales se pueden asociar a conveniencia y el resultado se mantendrá invariable), es conmutativa (el orden de los sumando no altera la suma , o resultado) y además existe el cero “0” que es neutro para la suma (+) en el conjunto de los naturales.

---

---

Sea el conjunto A, la siguiente tabla representa un ejemplo de un semigrupo en A.

---

---

---

---

---

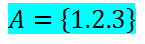
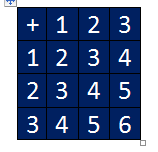
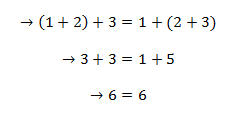
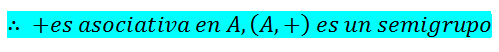
Hasta acá nuestro post del día. Hasta un nuevo encuentro amigos!!