ABORDAJE DIDÁCTICO DEL FENÓMENO DE CONSOLIDACIÓN UNIDIMENSIONAL DE LOS SUELOS DESDE UN ENFOQUE MATEMÁTICO CON BASAMENTO EN EL PRINCIPIO DE ESFUERZOS EFECTIVOS Y LA LEY DE PERMEABILIDAD DE DARCY. PARTE III

INTRODUCCIÓN

Este trabajo representa la capitalización de los esfuerzos realizados por el autor (ver ref. 03 y ref. 04) en aras de comprender el fenómeno de consolidación unidimensional de los suelos desde un enfoque matemático, con la intención de llegar a expresiones y gráficos de importancia práctica, para el abordaje de la consolidación desde una perspectiva experimental en un laboratorio de Mecánica de Suelos y la consecuente extrapolación de los resultados allí obtenidos al campo (escala real).

Imagen N°01: una visión global de las ideas a disertar en el presente trabajo

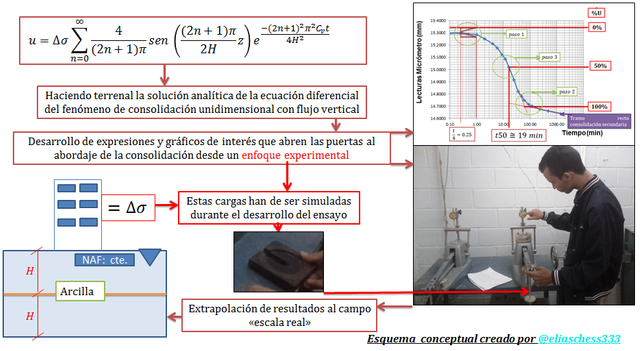
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. Las imágenes fueron capturadas con mi dispositivo Tablet VIT-T4000.

Para tal fin es necesario trabajar la expresión que rige la variación de la presión en exceso a la hidrostática “u” (ver imagen N°01) introduciendo conceptos de interés como el factor tiempo “T” y el grado de Consolidación “%U”, y aplicando técnicas básicas de integración, las cuales podremos apreciar en el desarrollo del presente trabajo.

DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR: AFIANCEMOS LAS HIPÓTESIS ESTABLECIDAS

En la referencia N°03 se explica detalladamente el procedimiento que permitió llegar a la ecuación diferencial que rige el fenómeno de consolidación unidimensional de los suelos con flujo de agua vertical:

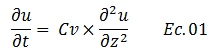
Por su parte, en la referencia N°04 se desarrolla la solución analítica que da por resultado la siguiente expresión:

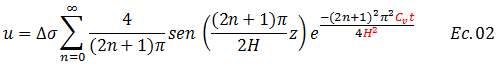
A partir de la ecuación N°02, desarrollaremos una serie de expresiones y gráficos de gran utilidad al momento de ejecutar el ensayo de Consolidación Unidimensional en un laboratorio de Mecánica de Suelos; reflexionemos en los conceptos e ideas involucradas que permitieron llegar a dicha ecuación.

Imagen N°02: una visión didáctica de la variación de “u” y el incremento de los esfuerzos efectivos “∆σ'”

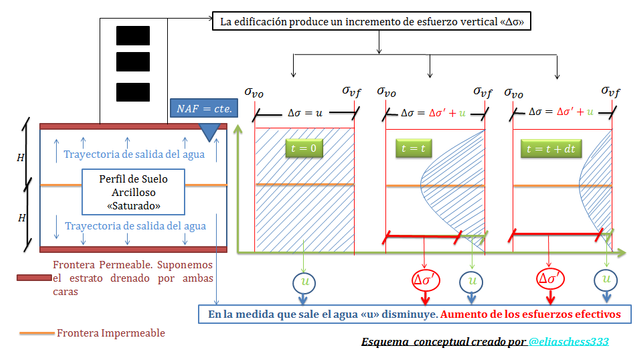
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.

Al observar detalladamente el esquema conceptual de la imagen N°02, se afianza la idea que la consolidación es un proceso de asentamiento que experimenta el suelo (arcilla), cuya evolución depende de la disipación de la presión en exceso a la hidrostática “u”, lo que incide en el incremento de los esfuerzos efectivos “∆σ’”. Surgen así las siguientes interrogantes:

¿Físicamente como interpretamos el concepto de esfuerzo efectivo?

Este concepto hace referencia al contacto efectivo entre las partículas de suelo. Destacando que la presencia de agua lo inhibe de alguna forma, de allí, que al irse disipando la presión en exceso de la hidrostática “u” este contacto aumenta, lo que redunda en la reducción de los vacíos. En el esquema conceptual de la imagen N°03 se ilustra de forma analítica un cálculo tipo de los esfuerzos efectivos “σ’” en el suelo.

¿Por qué el asentamiento ocurre diferido en el tiempo?

Recordemos que los suelos que tomamos como referencia en el estudio de este fenómeno son las arcillas, las cuales tienen una baja permeabilidad; esta propiedad hidráulica la podemos comprender como esa capacidad del suelo de permitir que el agua lo atraviese, en el caso de las arcillas, este proceso se dificulta, lo que origina que la expulsión gradual de agua que se ilustra en la imagen N°02 tarde mucho tiempo en producirse.

¿Qué hipótesis debemos tener en cuenta?

Es importante resaltar que el suelo se considera saturado durante todo el proceso de consolidación, lo que sugiere que la posición del nivel de aguas freáticas “NAF” no varía. En la medida que comienza la expulsión del agua, se supone que el flujo es laminar con sentido vertical. Por su parte “H” es considerado el espesor efectivo que recorre una gota de agua (ver imagen N°02).

Las respuestas a cada una de estas interrogantes, representan los fundamentos que Terzaghi estableció para la formulación de las ecuaciones N°01 y N°02. En este trabajo, se desarrollarán una serie de aplicaciones prácticas que ponen de manifiesto lo importante de la información obtenida en un laboratorio, para estimar cómo evolucionan los asentamientos en el tiempo, lo cual es clave conocer en todo proyecto de cimentaciones, donde hay presencia de suelos arcillosos. Es necesario destacar, que escapa del alcance de este trabajo, los cálculos concernientes a asentamientos; simplemente estaremos considerando un valor, para estimar la evolución de estos en el tiempo. En una próxima entrega se profundizará en el cálculo de los mismos.

HACIENDO TERRENAL LA SOLUCIÓN ANALÍTICA DE LA ECUACIÓN DIFERENCIAL DEL FENÓMENO DE CONSOLIDACIÓN UNIDIMENSIONAL

En primera instancia es necesario ampliar uno de los gráficos presentados en el esquema conceptual de la imagen N°02, relativos a la distribución de la presión en exceso a la hidrostática “u” con la profundidad para un determinado instante de tiempo:

Imagen N°03: interpretación gráfica del grado de consolidación “%U”

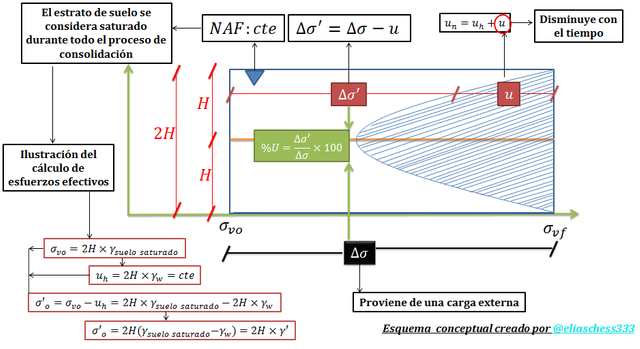
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.

Se desprende de la imagen N°03 una relación entre el incremento de los esfuerzos efectivos “∆σ’” y el incremento de los esfuerzos verticales “∆σ” producto de la aplicación de una carga externa, estos valores tenderán a ser iguales en un tiempo idealizado como infinitamente largo, dando así por finalizado un ciclo de consolidación primaria, caracterizado por la disipación de toda la presión en exceso a la hidrostática “u”. Estas ideas expuestas permiten introducir el concepto de grado de consolidación “%U”, el cual según Badillo y Rodríguez (2007):

Hace referencia a la consolidación que ha tenido lugar a una profundad en un instante de tiempo determinado, con respecto a la consolidación total que ha de producirse bajo el incremento de una carga impuesta. El grado de consolidación “%U” del estrato de suelo, es sólo una función del factor tiempo “T”, que es una cantidad sin dimensiones físicas.

La aseveración que estos autores hacen, encamina el proceso de obtención de expresiones de interés práctico, lo cual es el enfoque del presente artículo. No obstante, es necesario sustentar esta aseveración matemáticamente. En este sentido, el factor tiempo “T” viene dado por los términos resaltados en color “rojo” de la ecuación N°02:

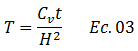
Dónde:

Cv, es el coeficiente de consolidación expresado en unidades de área sobre tiempo, por ejemplo “cm2/seg”.

t, es el tiempo en cual se evalúa el avance de la consolidación, expresado por ejemplo en “seg”.

H, es el espesor de estrato efectivo que recorre una gota de agua, expresado por ejemplo en “cm”.

Al sustituir estas unidades con sus respectivos valores unitarios en la ecuación N°03, podemos demostrar que el factor tiempo “T” es adimensional:

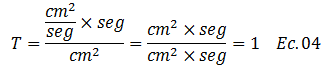
En este orden de ideas, la ecuación N°02 la podemos rescribir, aprovechando de cambiar el símbolo exponencial “e” por “ε”, con la finalidad de evitar confusiones con una propiedad índice de los suelos como lo es la relación de vacíos “e”.

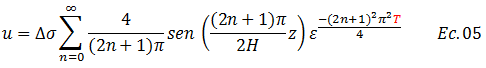
Ahora bien, para demostrar que el grado de consolidación “U” depende únicamente del factor tiempo “T”, definámoslo primero de forma matemática, con ayuda del gráfico de la imagen N°03, basados en la proporcionalidad que existe entre incremento de esfuerzos efectivos “∆σ’” e incremento de esfuerzos verticales “∆σ”, y considerando que “%U=100” cuando estos se igualan:

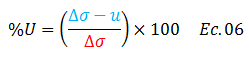
Es necesario a la ecuación N°06 darle una mayor rigurosidad matemática; de allí a que el término resaltado en color “azul” se extrapole a una profundidad “z” determinada del estrato en estudio, expresando la misma en términos de diferenciales, por lo que:

Para obtener “∆σ’” en todo el estrato, integramos de la siguiente manera:

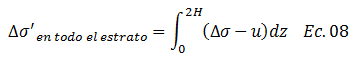
Por su parte el término resaltado en color “rojo” en la ecuación N°06, es representativo de todo el esfuerzo que debe soportar el suelo para consolidarse al “100%”, y proviene de una carga externa aplicada (ver imágenes N°01 y N°02) por lo que se considera constante en todo el proceso de consolidación. Esta hipótesis, permite extrapolar “∆σ” a todo el estrato, multiplicándolo por su espesor:

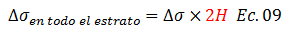
Donde “2H” representa el espesor de todo el estrato. Sustituyendo las ecuaciones N°08 y N°09 en la N° 06 obtenemos lo siguiente:

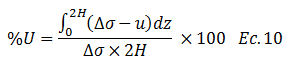
Rescribimos:

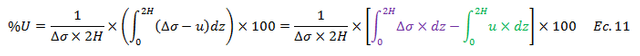
La integral resaltada por el color “púrpura” se resuelve a continuación, acotando que los términos resaltados en color “rojo” son los límites con respecto a los cuales se evaluará el resultado de la integral:

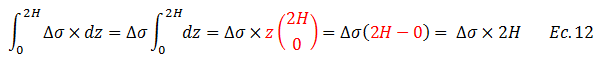
En lo referente a la integral resaltada en color “verde”, sustituimos en la misma la ecuación N°05, obteniendo lo siguiente:

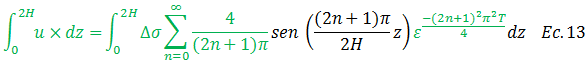
Los términos resaltados en color “verde” salen como constantes:

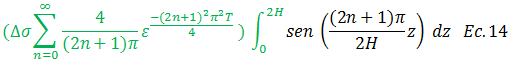
La integral de la ecuación N°14, se resuelve usando la técnica de sustitución, cuyo procedimiento se ilustra en el esquema conceptual de la imagen N°04:

Imagen N°04: aplicación de la técnica por sustitución

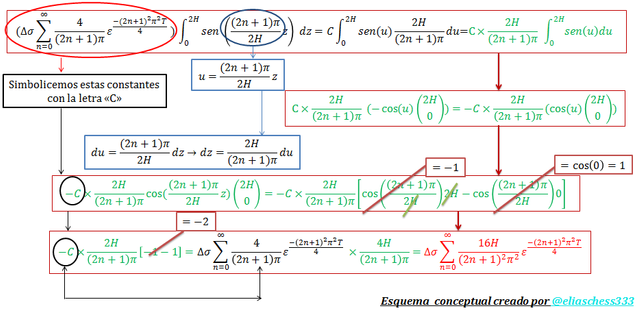
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.

Sustituimos el resultado resaltado en color “rojo” del esquema conceptual de la imagen N°04 y el resultado de la integral de color “púrpura” (Ec.12) en la ecuación N°11:

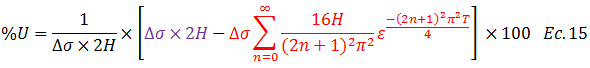
Aplicamos propiedad distributiva:

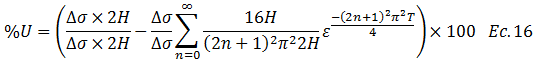
Rescribimos:

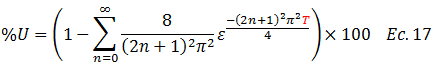
Demostrándose de este modo que el grado de consolidación depende del factor tiempo “T”. De tal manera que una forma de hacer terrenal esta expresión, es con el desarrollo de una gráfica que involucre el grado de consolidación “%U” y el factor en cuestión; de allí a que procedamos a evaluar la ecuación N°17 para distintos valores de “T”, desarrollando la sumatoria desde “n=0 a n=8”, lo cual es una solución un tanto aproximada; no obstante, al analizar las tablas que a modo de esquemas conceptuales se presentan a lo largo de las imágenes N°05, N°06, N°07, N°08, N°09,N°10 y N°11, el aporte a la sumatoria “∑” para valores de “n” de orden superior es bastante pequeño.

Imagen N°05: evaluación de la ecuación N°17 para T=0.000 y T=0.004

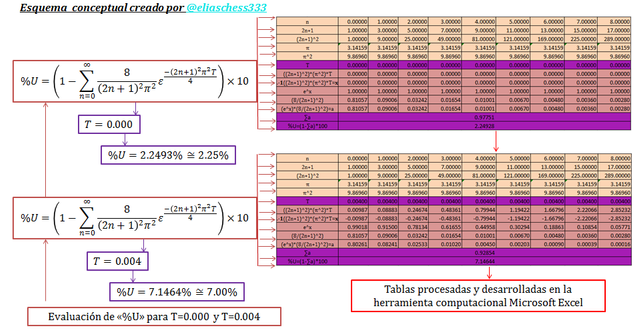
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. La data que contiene la tabla fue desarrollada con ayuda de la herramienta Microsoft Excel.

Imagen N°06: evaluación de la ecuación N°17 para T=0.008 y T=0.031

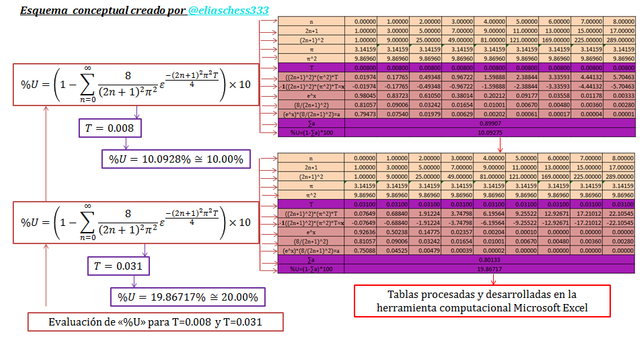
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. La data que contiene la tabla fue desarrollada con ayuda de la herramienta Microsoft Excel.

Imagen N°07: evaluación de la ecuación N°17 para T=0.071 y T=0.126

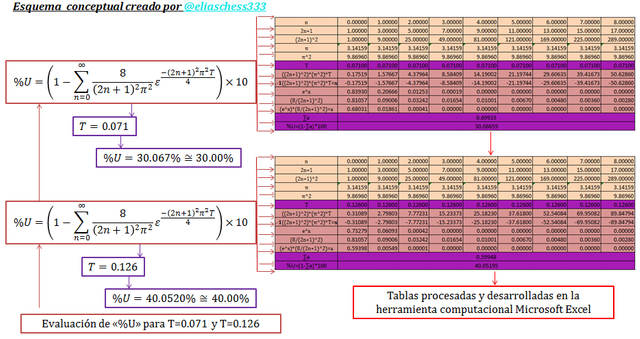
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. La data que contiene la tabla fue desarrollada con ayuda de la herramienta Microsoft Excel.

Imagen N°08: evaluación de la ecuación N°17 para T=0.197 y T=0.287

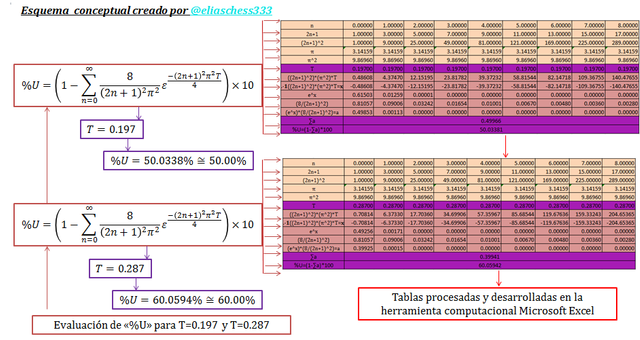
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. La data que contiene la tabla fue desarrollada con ayuda de la herramienta Microsoft Excel.

Imagen N°09: evaluación de la ecuación N°17 para T=0.405 y T=0.565

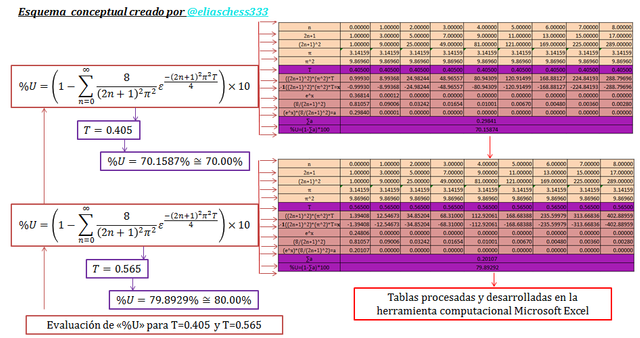
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. La data que contiene la tabla fue desarrollada con ayuda de la herramienta Microsoft Excel.

Imagen N°10: evaluación de la ecuación N°17 para T=0.848 y T=2.000

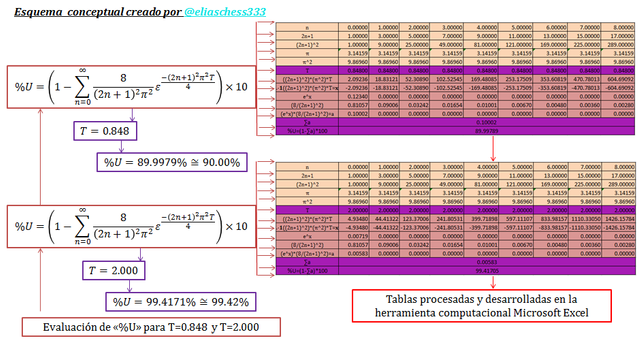
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. La data que contiene la tabla fue desarrollada con ayuda de la herramienta Microsoft Excel.

Imagen N°11: evaluación de la ecuación N°17 para T=6.000 y T=10.000

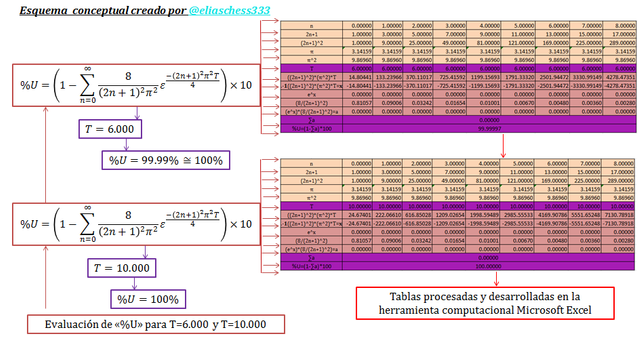
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. La data que contiene la tabla fue desarrollada con ayuda de la herramienta Microsoft Excel.

Para los propósitos que sigue, la información de relevancia de los esquemas conceptuales presentados, corresponde a los distintos valores de “%U” y “T” por lo que presento a continuación un esquema conceptual, en el que se hace una tabla resumen de estos resultados con su respectiva gráfica, teniendo la precaución de configurar el eje de las abscisas en escala logarítmica, y el eje de las ordenadas en escala natural.

Imagen N°12: curva teórica de consolidación

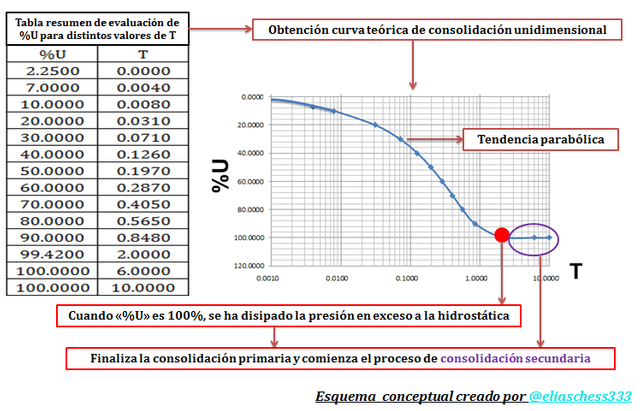
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. La data que contiene la tabla y el gráfico, fueron desarrollados con ayuda de la herramienta Microsoft Excel.

La gráfica anteriormente presentada abre las puertas al abordaje del estudio de la consolidación desde una perspectiva experimental en un laboratorio, para su posterior vinculación con las labores de campo, donde estén involucrados suelos de naturaleza arcillosa, como por ejemplo, en un proyecto de cimentaciones.

APLICACIONES PRÁCTICAS: NOCIONES GENERALES SOBRE EL ENSAYO DE CONSOLIDACIÓN

En primer lugar, es importante señalar que el ensayo de consolidación de los suelos es realizado con un equipo conocido como “Consolidómetro”.

Imagen N°13: nociones generales de la consolidación desde un enfoque experimental

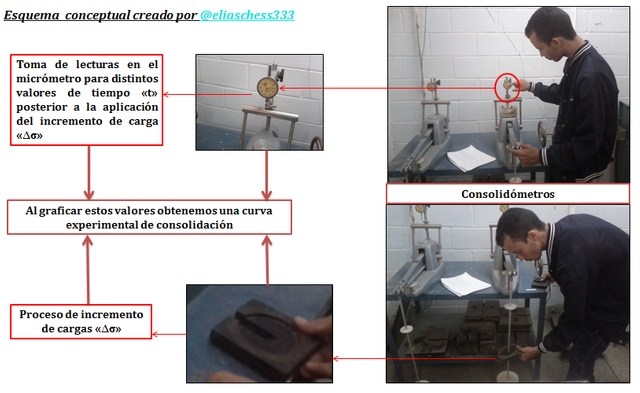
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. Las imágenes fueron capturadas con mi dispositivo Tablet VIT-T4000.

De acuerdo a lo que se aprecia en la imagen N°13, los incrementos de carga que se realizan en el desarrollo del ensayo, deben buscar simular las cargas reales a las que estará sometido el estrato arcilloso en campo (escala real), para que el ensayo sea representativo.

APLICACIONES PRÁCTICAS: OBTENCIÓN DE LA CURVA EXPERIMENTAL DE CONSOLIDACIÓN Y ESTIMACIÓN DEL “T50”

Tomemos como referencia una data experimental para un determinado incremento de carga. A partir de allí se procede a realizar la curva experimental de consolidación, graficando en las abscisas los valores de tiempo en “minutos” (escala logarítmica), y en las ordenadas las lecturas arrojadas por el micrómetro en “mm” (escala natural). Una vez obtenida la curva experimental de consolidación, procedemos a aplicar el método gráfico de Casagrande para la obtención del “t50”.

Imagen N°14: curva experimental de consolidación. Ilustración gráfica obtención del “t50”

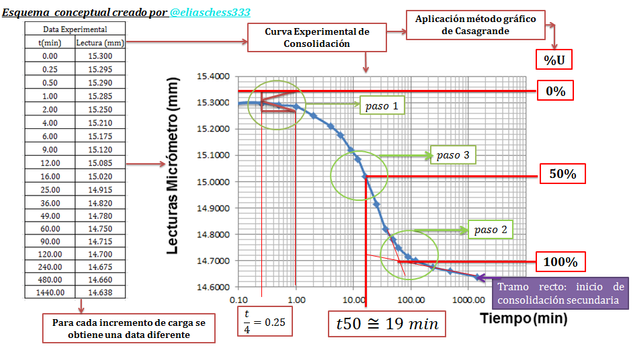
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. La data que contiene la tabla y el gráfico, fueron desarrollados con ayuda de la herramienta Microsoft Excel.

Tomando como referencia la imagen N°14, el “paso 1” para la obtención del “t50”, es definir en la gráfica el punto teórico de “0%” de consolidación primaria. Para tal fin, seleccionamos arbitrariamente un tiempo que esté visualmente muy por debajo de la mitad de la curva, o simplemente, que esté al comienzo del tramo de la curva donde comenzamos a observar la mayor inclinación, a partir de este tiempo se extiende una línea vertical que intercepta la gráfica. Posterior a ello, se divide este tiempo por 4, es decir:

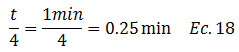
Este otro tiempo intercepta también la curva. Se aprecia en la imagen N°14, como estas intercepciones permiten dibujar un triángulo rectángulo, este triángulo se rebate, constituyendo la referencia para trazar una línea horizontal que representa el “0%” de la consolidación primara, surgiendo así, un eje de ordenadas alternativo a las lecturas del micrómetros, y que es una forma de vincular la curva teórica de consolidación con la experimental. Para obtener el “100%” de la consolidación primaria “paso 2” se proyecta el tramo recto de la consolidación secundaria (ver imagen N°14), y el mismo se intercepta con una recta que prolonga el tramo inclinado de la consolidación primaria. A partir de esta intercepción se traza una línea horizontal equivalente a “%U=100”.

Una vez construido este eje alternativo de grados de consolidación “%U”, el cual se encuentra acotado entre el “0%” y el “100%”, se traza una línea horizontal justo en la mitad “%U=50%” que intercepta la curva, y de aquí sale una línea vertical que intercepta el eje de las abscisas. El tiempo que allí se obtiene es el “t50”, el cual para el ejemplo que estamos considerando es de aproximadamente de diecinueve minutos (t50=19min=1140 segundos).

APLICACIONES PRÁCTICAS: ESTIMACIÓN DE LA EVOLUCIÓN DE LOS ASENTAMIENTOS EN EL TIEMPO

Para este fin, tomamos como referencia la ecuación N°03, suponiendo un espesor efectivo “H” que ha de recorrer una gota de agua en el desarrollo del ensayo de consolidación de “0.8640 cm”. Es válida la siguiente pregunta:

¿Y por qué un valor tan pequeño?

Y la respuesta a esta interrogante está en los implementos utilizados en el ensayo de consolidación, específicamente el anillo (ver imagen N°15) donde va la muestra de suelo, el cual típicamente posee una altura total “2H=2cm; y si se considera el estrato drenado por ambas caras “H=1cm”.

Imagen N°15: una breve antesala al estudio de la consolidación desde un enfoque experimental

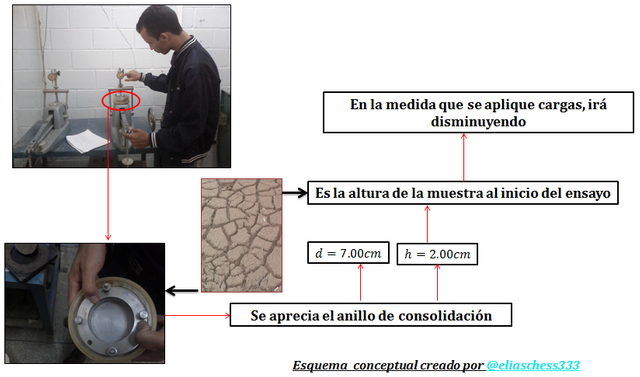
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. Las imágenes fueron capturadas con mi dispositivo Tablet VIT-T4000.

¿Y a qué se debe que no utilicemos el valor de “H=1cm” sino el de “H=0.864cm”?

Es evidente que en la medida que se van aplicando cargas, la altura “H” de la muestra de suelo va disminuyendo. En una próxima entrega estaré profundizando en el proceso de obtención de esta información en un laboratorio. Por lo que ahora concierne, que es la demostración de la aplicabilidad del “t50”, tenemos que para “%U=50” corresponde un “T=0.197”; toda esta información descrita permite rescribir la ecuación N°03:

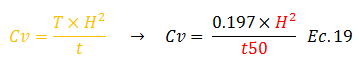
Sustituimos los datos conocidos:

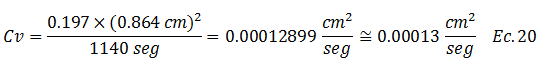
Conocido el coeficiente consolidación “Cv” el cual suponemos constante durante todo el proceso de consolidación que produce un incremento de carga determinado “∆σ”, estamos listos para estimar la evolución de los asentamientos en el tiempo. Tomando como referencia el gráfico de la imagen N°03, basémonos en los siguientes datos, que hacen referencia a un estrato arcilloso en escala real.

• 2H=400 cm
• H=200 cm
• Asentamiento total por consolidación primaria=10 cm

Este último dato, señala el asentamiento total que experimenta el estrato arcilloso, una vez se haya disipado toda la presión en exceso a la hidrostática “u”. Dado que deseamos estimar la evolución del asentamiento en el tiempo “t”, de la expresión resaltada en color naranja de la ecuación N°19, podemos despejar esta variable de la siguiente forma:

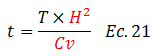
Sustituimos los datos conocidos y dejamos la ecuación N°21 en función del factor tiempo “T”:

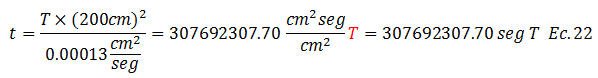
El tiempo lo podemos llevar a una escala de días:

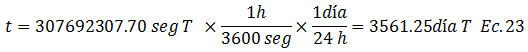
A partir de la información presentada en el esquema conceptual de la imagen N°12 y usando la ecuación N°23, el estudio de la evolución de los asentamientos en tiempo, se ilustra a continuación:

Imagen N°16: estudio de la evolución de los asentamientos en el tiempo

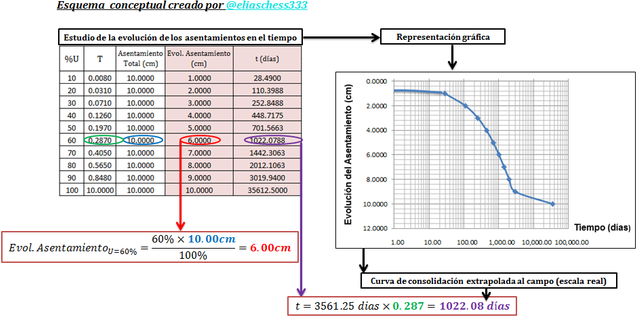
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. La data que contiene la tabla y el gráfico, fueron desarrollados con ayuda de la herramienta Microsoft Excel.

Significa entonces, que un asentamiento de “6cm” en el estrato arcilloso en consideración, tendrá lugar en un tiempo de “1022.08 días”, es decir, casi tres años han de pasar para que se produzca tal asentamiento. Esto es una visión práctica de las ideas expuestas anteriormente, acerca el fenómeno de consolidación, demostrándose que tanto puede tardar, el desarrollo de las deformaciones en una arcilla, como consecuencia de la aplicación de una carga externa.

CONCLUSIONES

En todo proyecto de cimentaciones, el conocimiento de los asentamientos que experimentara el suelo es fundamental, y aun más, cuando el estrato de suelo involucrado es una arcilla cuyos asentamientos ocurren diferidos en el tiempo. Hasta este momento, hemos promovido el desarrollo de un sentido crítico hacia la solución analítica de la ecuación diferencial de consolidación unidimensional, a través del desarrollo de herramientas prácticas, que permiten vincular las labores de un laboratorio de mecánica de suelos, con el campo (escala real); por ejemplo, el gráfico de la imagen N°16 es de gran importancia práctica, dado que para unas condiciones de carga determinadas, podemos saber el asentamiento por consolidación que experimentará la arcilla para un tiempo dado. A continuación un resumen de las principales conclusiones de este artículo:

1.- El grado de consolidación “%U” que experimenta un estrato arcilloso depende del factor tiempo “T”.

2.-La obtención del “t50” se logra por métodos gráficos, aplicados a la curva experimental de consolidación.

3.-La obtención del “t50” permite calcular el coeficiente de consolidación “Cv” el cual se considera constante para la consolidación que produce un determinado incremento de carga.

4.- La curva teórica de consolidación, es de gran utilidad para estudiar la evaluación de los asentamientos en el tiempo.

Representa un reto en todo proyecto de cimentaciones, la presencia de suelos de naturaleza arcillosa; de allí la importancia del estudio de estos, siendo una de las muestras de este hecho el ensayo de consolidación que se realiza en un laboratorio de Mecánica de Suelos, sobre el cual se dio una breve antesala en este artículo, y en el que profundizaré en una próxima entrega.

Escribió para ustedes

@eliaschess333

FUENTES DE INFORMACIÓN CONSULTADAS

1.- BADILLO J. Y RODRÍGUEZ R. 2007. MECÁNICA DE SUELOS TOMO I. FUNDAMENTOS DE LA MECÁNICA DE SUELOS. EDITORIAL LIMUSA S.A. GRUPO NORIEGA EDITORES

2.- BADILLO J. Y RODRÍGUEZ R. 1995. MECÁNICA DE SUELOS TOMO III. FLUJO DE AGUA EN LOS SUELOS. EDITORIAL LIMUSA S.A. GRUPO NORIEGA EDITORES

LECTURAS RECOMENDADAS

3.- SANTANA E. 2018. ABORDAJE DIDÁCTICO DEL FENÓMENO DE CONSOLIDACIÓN UNIDIMENSIONAL DE LOS SUELOS DESDE UN ENFOQUE MATEMÁTICO CON BASAMENTO EN EL PRINCIPIO DE ESFUERZOS EFECTIVOS Y LA LEY DE PERMEABILIDAD DE DARCY. PARTE I. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/ozrzfpbw

4.- SANTANA E. 2018. ABORDAJE DIDÁCTICO DEL FENÓMENO DE CONSOLIDACIÓN UNIDIMENSIONAL DE LOS SUELOS DESDE UN ENFOQUE MATEMÁTICO CON BASAMENTO EN EL PRINCIPIO DE ESFUERZOS EFECTIVOS Y LA LEY DE PERMEABILIDAD DE DARCY. PARTE II. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/abordaje-didactico-del-fenomeno-de-consolidacion-unidimensional-de-los-suelos-desde-un-enfoque-matematico-con-basamento-en-el