INTRODUCCIÓN
A continuación vamos a realizar un abordaje práctico, de los principales aportes de las Matemáticas, al campo de la Dinámica de Estructuras, en lo concerniente al estudio de la técnica de condensación de la matriz de rigidez y la solución de una ecuación diferencial lineal homogénea de segundo orden, que permite encontrar las relaciones fundamentales para determinar periodo natural y frecuencia natural de la estructura que se analiza, sujeta a un régimen de vibración libre sin amortiguamiento, como se aprecia en la imagen N°01, observándose al mismo tiempo los casos de estudio, que difieren esencialmente en la cantidad de grados de libertad estáticos, dado que para fines prácticos se establecen la mismas secciones de las barras en cada uno de los casos, y arbitrariamente se define que el valor de la masa distribuida “m” del caso N°02 sea igual a la sumatoria de las masas puntuales del caso N°1; esto con la finalidad de contrastar cómo las propiedades dinámicas anteriormente citadas de periodo y frecuencia, son sensibles a las variaciones de rigidez lateral que se presentan entre los casos estudiados, lo cual se demostrará con ejemplos prácticos al final de este artículo.
Imagen N°01: casos en estudio sujetos a régimen de vibración libre sin amortiguamiento
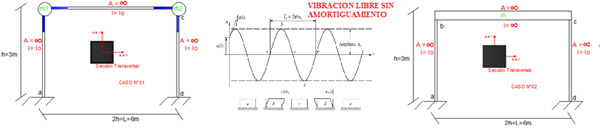
Fuente: Chopra (2014) adaptada por Santana (2018)
DELIMITACIÓN DE CASOS EN ESTUDIO. AFIANZANDO LA TÉCNICA DE CUANTIFICACIÓN DE GRADOS DE LIBERTAD ESTÁTICOS Y GRADOS DE LIBERTAD DINÁMICOS
Es necesario acotar, que en el presente trabajo el cálculo del período natural y frecuencia natural está delimitado a sistemas de un grado de libertad tanto estático como dinámico; de allí a que sea necesario distinguir las diferencias entre uno y otro. En este orden de ideas, los grados de libertad estáticos son las coordenadas necesarias para definir la posición de las juntas, y los grados de libertad dinámicos, aquellos necesarios para definir la posición de las masas. En la imagen N°02, podemos apreciar el proceso de cuantificación de los grados de libertad, para un pórtico plano, cuyos elementos presentan rigidez axial infinita (A) = ∞, es decir, no se permite alargamiento ni acortamiento.
Imagen N°02: representación de grados de libertad estáticos y dinámicos. Caso N°01
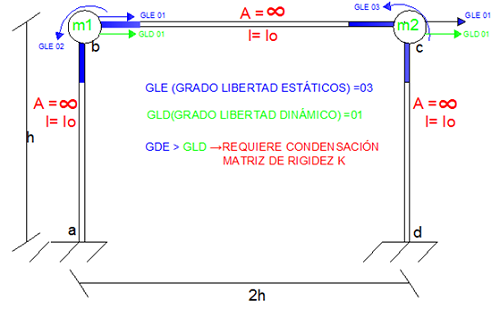
Fuente: Santana (2018)
En el pórtico de la imagen N°02 (caso N°01) se tienen dos masas concentrada (m1 y m2). Una masa concentrada se caracteriza por poseer dos grados de libertad dinámicos en el plano (ver imagen N°03), como lo son la traslación en el eje “X” y en el eje “Y”. La traslación de las masas “m1 y m2” no está permitida en el eje “Y”, puesto que para el caso N°01 implicaría un alargamiento de las barras “a-d” y “c-d” respetivamente; no obstante en el eje “X”, la traslación está permitida siempre y cuando exista compatibilización de los movimientos en esa dirección de “m1” y “m2”, dado que un movimiento independiente de estas, podría originar un acortamiento o alargamiento de la barra “b-c”, por lo tanto, el sistema posee un grado de libertad dinámico.
Imagen N°03: grados de libertad dinámicos de una masa concentrada
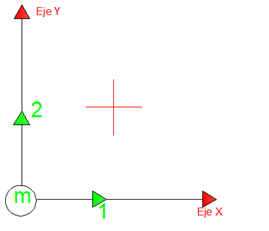
Fuente: Santana (2018)
En lo referente a los grados de libertad estáticos, se tiene que una junta en el plano (ver imagen N°04), tiene tres posibilidades de movimiento, como lo son la traslación en el eje “X”, en el eje “Y”, y la rotación como cuerpo rígido.
Imagen N°04: grados de libertad estáticos en una junta
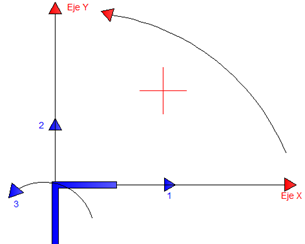
Fuente: Santana (2018)
Para el caso N°01 la traslación en el eje “Y” no está permitida porque implicaría un alargamiento de las barras verticales, y la traslación en el eje “X” si es posible, siempre y cuando exista una compatibilización de desplazamiento entre las juntas; es decir, estas no se pueden desplazar a lo largo del eje “X” de forma independiente, porque este hecho pudiese provocar un acortamiento o alargamiento de la barra “b-c” y el mismo no está permitido. Adicional al grado de libertad estático en la dirección “X”, se presentan las rotaciones de las juntas como cuerpo rígido; lo cual origina deformación transversal en las barras, la cual si está permitida, dado que la inercia no es infinita.
Otro caso de interés que estaremos abordando, es cuando la cantidad de grados de libertad estáticos coincide con la cantidad de grados de libertad dinámicos, como el que se muestra en la siguiente imagen:
Imagen N°05: pórtico plano con barra horizontal idealizada como cuerpo rígido. Caso N°02
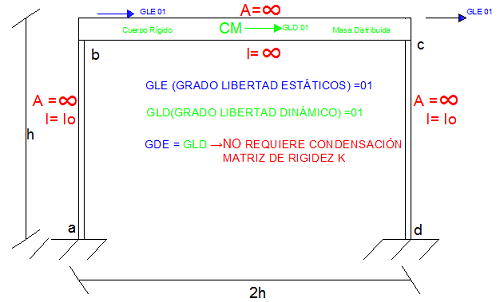
Fuente: Santana (2018)
En este caso existe un grado de libertad estático, representado por la traslación compatibilizada de las juntas en el eje “X; por su parte, la rotación de las juntas no está permitida, porque al tratarse la barra horizontal de un cuerpo rígido, no presenta deformación axial ni transversal, por lo que si una junta rotara provocaría el movimiento de todo el cuerpo rígido, originando un alargamiento de una de las barras; esto se ilustra en la imagen N°06:
Imagen N°06: ilustración del porqué la rotación en el nodo b, no está permitida
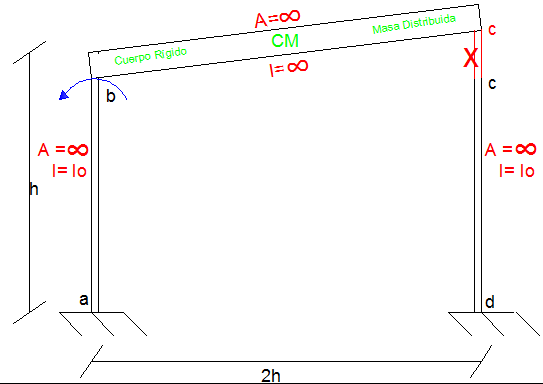
Fuente: Santana (2018)
En cuanto a los grados de libertad dinámicos, un cuerpo rígido como el de la imagen N°07 (caso N°02), se caracteriza por poseer en el plano tres grados de libertad dinámicos; y por no permitir deformación axial ni transversal. Los grados de libertad dinámicos se colocan en el extremo de la barra; destacando que estos pueden ser ubicados en cualquier parte de la misma, por ejemplo en su centro de masa CM. No obstante se colocan allí para aprovechar la imagen N°06, e ilustrar así, lo que pasaría si se activa el grado de libertad dinámico asociado a la rotación, que provocaría un alargamiento de la barra “c-d”. Situación similar ocurriría si se activa el grado de libertad dinámico asociado a la traslación vertical, produciendo el alargamiento de la barra “a-b”.
Imagen N°07: grados de libertad dinámicos en un cuerpo rígido
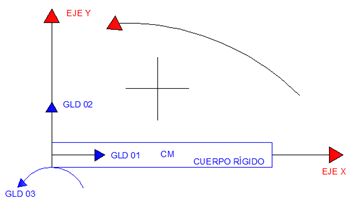
Fuente: Santana (2018)
De tal manera que el sistema presentado en la imagen N°05, posee un grado de liberad estático y un grado de libertad dinámico, es decir, no es necesario realizar condensación de matriz de rigidez.
DESARROLLO DE LA ECUACIÓN DE EQUILIBRIO DINÁMICO DEL SISTEMA. CASO N°1
En base a los planteamientos anteriormente señalados, el sistema presenta tres grados de libertad estáticos y un solo grado de libertad dinámico; esta situación se aborda en el tópico concerniente a “APRENDIENDO A CONDENSAR LA MATRIZ DE RIGIDEZ K” donde se obtendrá el valor de rigidez lateral del sistema, acorde a la aceleración que experimentan la masas (m) = m1 + m2, al activarse el grado de libertad dinámico en el eje “X”. Todo este planteamiento sugiere el desarrollo de una ecuación de equilibrio dinámico, en la que intervengan fuerzas inerciales (fi), y fuerzas de restitución elástica (fs), que se opondrían a la aceleración (ü) y desplazamiento (u) respectivamente, producto de una carga externa aplicada en la dirección “X”, de este modo:

Aplicando el principio de D’Alembert, se plantea la ecuación general de equilibrio dinámico de la forma (ver diagrama de cuerpo libre de la imagen N°08):
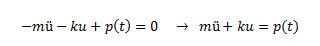
Imagen N°08: diagrama de cuerpo libre “principio de D’Alembert”. Caso N°01.
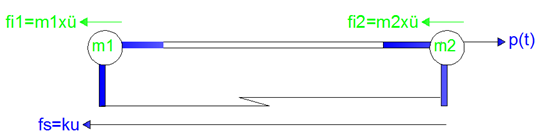
Fuente: Santana (2018)
Dado que se desea encontrar las ecuaciones para la estimación de periodo natural y frecuencia natural, se considera al sistema en un régimen de vibración libre sin amortiguamiento, la cual según Chopra (2014), consiste en perturbar la estructura de su posición de equilibrio estático, y dejarla vibrar sin ninguna excitación dinámica externa, es decir, p(t) = 0; por lo que la ecuación de equilibrio dinámico planteada se puede rescribir de la forma:
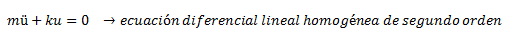
DESARROLLO DE LA ECUACIÓN DE EQUILIBRIO DINÁMICO DEL SISTEMA. CASO N°2
En el caso N°02 no se requiere obtener matriz de rigidez puesto que se tiene un grado de libertad estático, el procedimiento se limita a determinar el aporte de la rigidez lateral de cada una de las barras verticales; lo cual se desarrolla en el tópico concerniente a “ESTUDIO DE CASO DONDE NO SE REQUIERE CONDENSACIÓN DE MATRIZ K”.
Ahora bien, similar a lo que sucede en el caso N°01, en el desarrollo de la ecuación de equilibrio dinámico, intervienen fuerzas inerciales (fi), y fuerzas de restitución elástica (fs), que se opondrían a la aceleración (ü) y desplazamiento (u) respectivamente, producto de una carga externa aplicada en la dirección “X” (ver imagen N°09). Por lo tanto:

Imagen N°09: diagrama de cuerpo libre “principio de D’Alembert”. Caso N°02.

Fuente: Santana (2018)
Partiendo de la misma suposición de vibración libre sin amortiguamiento hecha para el caso N°01, la ecuación de equilibrio dinámico que se obtiene es la misma.
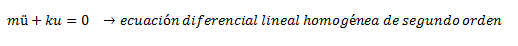
SOLUCIÓN ANALÍTICA DE LA ECUACIÓN DIFERENCIAL DE EQUILIBRIO DINÁMICO
De acuerdo a las características de la ecuación diferencial en estudio, podemos introducir dos posibles soluciones:
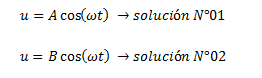
Para sustituir una de las soluciones, en la ecuación diferencial de equilibrio dinámico, es necesario determinar su segunda derivada, lo cual se realiza a continuación tomando como referencia la solución N° 01:
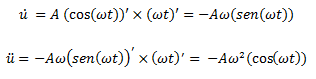
Al sustituir en la ecuación diferencia se tiene lo siguiente:
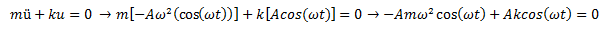
Sacamos factor común:
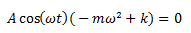
Para que esta ecuación se satisfaga en cualquier instante de tiempo:
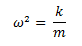
Encontrando de esta manera la relación para determinar la frecuencia natural del sistema:
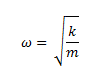
Ahora bien, para desarrollar una mejor visión en el significado físico del período (T), solucionemos la ecuación de equilibrio dinámico, fundamentándonos en el hecho de que podemos superponer las dos soluciones antes descritas, lo cual por tratarse de una ecuación diferencial lineal está permitido, y por poseer esta solución dos constantes de integración “A” y “B”, puede ser considerada como la solución general de la ecuación diferencial en estudio.
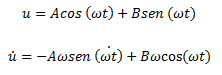
A y B, son variables conocidas del sistema, como el desplazamiento (u) y la velocidad (ů) , las cuales al perturbarse la posición de equilibrio en el instante de tiempo t=0, toman valores iniciales; si establecemos lo siguiente:
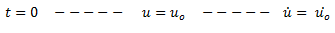
Y sustituimos en la solución general tanto de desplazamiento como de velocidad podemos obtener los valores de A y B:
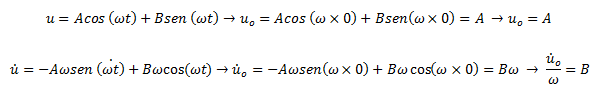
Sustituyendo estas variables de condición inicial en la solución de desplazamiento general se tiene:
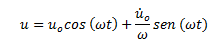
La representación gráfica de esta solución la podemos observar en la siguiente imagen:
Imagen N°10: vibración libre de un sistema sin amortiguamiento
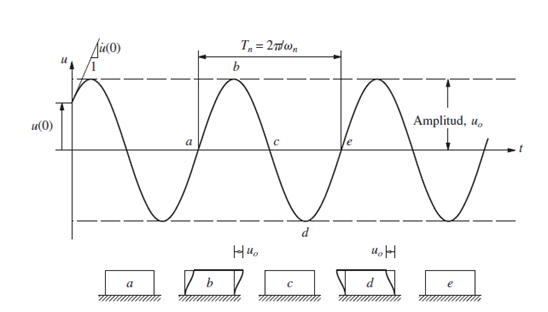
Fuente: Chopra (2014).
En la imagen mostrada se aprecia, que el movimiento es armónico y por lo tanto periódico; adicionalmente el periodo (T) de una función seno o coseno es de 2(π), por lo que:
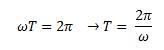
Vale destacar que el periodo mide el tiempo en completarse un ciclo; y tiene su recíproco que es la frecuencia la cual mide la cantidad de ciclos en una unidad de tiempo. Conviene señalar que existen dos formas de representar la frecuencia:
Forma N°01: frecuencia angular (ω), unidades son radianes por segundo (rad/seg)
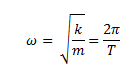
Forma N°02: frecuencia natural (f), son unidades son ciclos por segundo (cps) o hercios (hz)
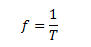
Cada una de estas propiedades dinámicas a menudo se acompañan del sufijo “n” (ver imagen N°10), para hacer énfasis que dependen de la masa (m) y rigidez (K) del sistema estructural, resaltando la importancia del cálculo correcto de estas propiedades naturales. En los tópicos que siguen se determinará este valor de rigidez “K” ajustado a los casos de estudio.
APRENDIENDO A CONDENSAR LA MATRIZ DE RIGIDEZ K
Es preciso señalar que el proceso de condensación de la matriz de rigidez K, se realiza cuando el número de grados de libertad estáticos supera los grados de libertad dinámicos, tal situación la podemos apreciar en el caso N°01 (ver imagen N°02).
De manera general se puede establecer la siguiente ecuación de equilibrio dinámico en términos matriciales, partiendo de la suposición de la existencia de una carga dinámica aplicada en la dirección del grado de libertad de la masa.
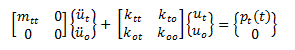
Se tiene que “uo” son los grados de libertad estáticos sin masa asociada, mientras que “ut” representa los grados de libertad estáticos con masa asociada. Ahora bien, el desarrollo de las operaciones matriciales básicas, permite obtener las siguientes ecuaciones:
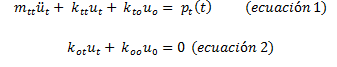
Despejamos de “ecuación 2” el término uo, obteniendo lo siguiente:
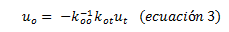
Sustituimos la “ecuación 3” en “ecuación 1”, de la forma:
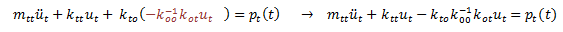
Si sacamos factor común:
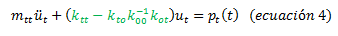
Representando los términos resaltados en color verde la matriz de rigidez condensada, la cual se puede representar de la forma:
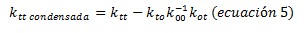
Una vez deducida estas expresiones, procedemos a aplicarlas al caso N°01 (ver imagen N°02), representado por un pórtico plano con tres grados de libertad estáticos y un grado de libertad dinámico. El autor (ver ref.03), establece que la matriz de rigidez K para este caso en estudio, asumiendo que las barras tienen las mismas propiedades de inercia y área, es la siguiente:
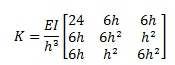
En lo que respecta a las masas puntuales “m1 y m2”, las podemos totalizar en una sola, con el símbolo “m”; la cual por poseer un grado de libertad dinámico en la dirección “X”, no requiere del uso de matrices, dado que de la misma forma como la cantidad de grados de libertad estáticos influyen en el tamaño de la matriz de rigidez, igual influencia tienen los grados de libertad dinámicos en la matriz de masa.
Ahora bien, en aras de aplicar la ecuación 5, la matriz de rigidez K, se puede plasmar de la siguiente manera:
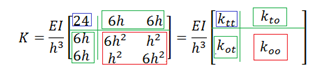
Por lo que la matriz de rigidez condensada se obtiene a partir de:
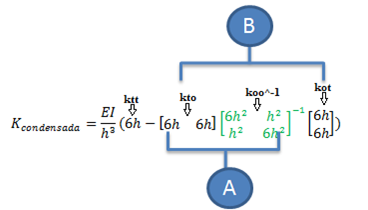
Como podemos apreciar, es necesario, calcular la inversa de la matriz resaltada en color verde, lo cual se logra ampliando el sistema matricial con una matriz diagonal, y realizando operaciones de suma, resta, multiplicación entre las filas de la matriz ampliada, hasta convertir la matriz a la cual se le quiere obtener su inversa en una matriz diagonal, y por consiguiente la nueva matriz que surge en el lado derecho del sistema ampliado, representa la inversa de la matriz en estudio. A continuación se ilustra de forma didáctica este procedimiento:
Imagen N°11: ilustración didáctica del proceso para encontrar una matriz inversa de orden 2x2
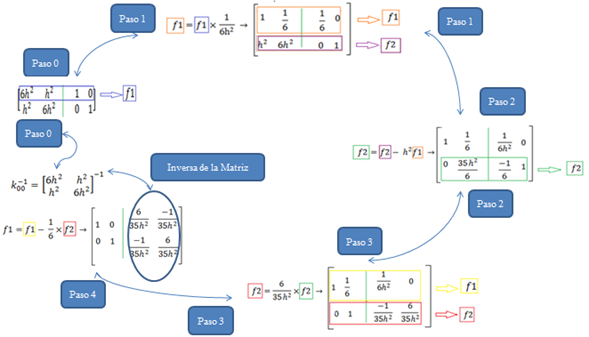
Fuente: Santana (2018)
En resumen se tiene lo siguiente:
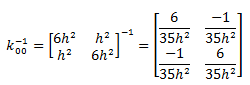
Procedemos ahora a realizar el producto matricial:
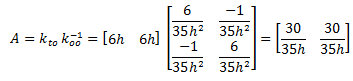
Obtenemos ahora el componente B de la ecuación N°05:
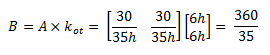
Restamos el “ktt” al componente B, para encontrar la matriz condensada:
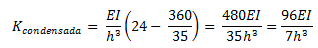
Como podemos apreciar, la matriz condensada se reduce a un elemento, que depende de la altura (h), de la inercia de la sección transversal (I) y del módulo de elasticidad (E); y este hecho no debe de parecernos extraño, dado que como se tiene un grado de libertad dinámico, se espera entonces que al hacer la condensación de la matriz de rigidez, se obtenga un elemento, que representa la rigidez lateral del pórtico estudiado (ver imagen N°02).
Resulta de mucho interés contrastar dicha rigidez lateral, con el caso N°02 (imagen N°05), en el cual no se requiere condensación de la matriz de rigidez K.
ESTUDIO DE CASO DONDE NO SE REQUIERE CONDENSACIÓN DE MATRIZ K
Al tratarse de un sistema con un grado de libertad estático, se obtiene es un elemento que representa la rigidez lateral del pórtico, es decir:
Imagen N°12: desplazamiento unitario, producto de aplicar una fuerza de corte “V”
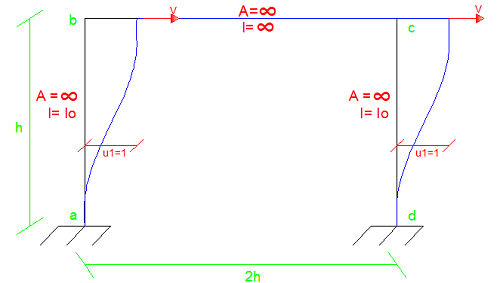
Fuente: Santana (2018)
Aplicando el método de coeficientes de rigidez para un elemento a flexión (ver ref. 03), se obtiene lo siguiente:
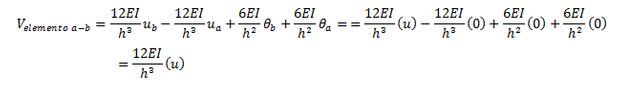
Donde “u” es un desplazamiento unitario, y partiendo de la expresión general de esfuerzo cortante, que establece:
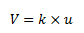
Se tiene que la rigidez lateral de la barra “a-b” es la resaltada por el ovalo de color rojo:
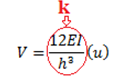
Y dado que la barra “c-d” contribuye de la misma manera que la barra “a-b” a la rigidez lateral del sistema estructural, se tiene por lo tanto que la rigidez global es:
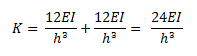
Al contrastar esta rigidez, con la obtenida para el caso N°01:

Nos damos cuenta, que la presencia del cuerpo rígido, permite incrementar la rigidez lateral del sistema estructural, lo cual es lógico debido a que para el caso N°01, la rigidez lateral se ve disminuida, por la deformación transversal que presenta la barra horizontal.
Aclarados estos aspectos procedamos a cuantificarlos con ejemplos prácticos, prestando especial atención, en la influencia de la rigidez lateral en los valores de periodo natural y frecuencia natural, lo cual se aborda en el siguiente tópico.
DESARROLLO DE EJEMPLOS PRÁCTICOS
Recordemos los casos en estudio, tomando como referencia la imagen N°13:
Imagen N°13: representación de los casos en estudio
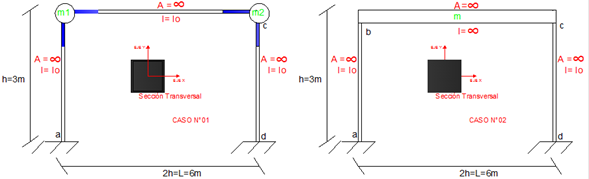
Fuente: Santana (2018)
Para ambos casos se tiene que:
Módulo de Elasticidad E= 240000 kgf/cm2
Sección transversal cuadrada, de lados de 50.00 cm de longitud (ver imagen N°14)
Imagen N°14: sección transversal de las barras que constituyen el pórtico
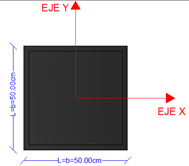
Fuente: Santana (2018)
Dado que es la misma sección para ambos casos, el valor de inercia (I) también es un dato en común. Por tratarse de una sección cuadrada Ix=Iy, este valor se puede calcular de la siguiente manera:
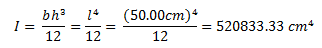
En lo que respecta a la propiedad de masa de los sistemas estructurales en estudio, conviene señalar que si nos dieran como dato el peso (W), la masa (m) se obtiene partiendo de la siguiente fórmula:
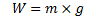
Dónde “g” corresponde a la aceleración de gravedad.
Para el caso N°01, estableceremos que W1 = W2 = 750000.00 kgf, por lo tanto:
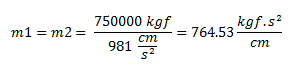
Siendo el valor de masa total que participa en la estimación de las propiedades dinámicas de período y frecuencia la suma de m1 y m2.
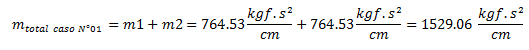
La masa distribuida del caso N°2, se le asigna un valor arbitrario de:
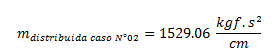
Como se puede apreciar en los cálculos de periodo y frecuencia natural, para ambos casos en estudio, participará la misma masa; esto se hace intencionalmente, para demostrar el efecto de la rigidez en estas propiedades dinámicas que se desean obtener, cuyo cálculo se puede apreciar en la tabla N°01:
Tabla N°01: estimación de período y frecuencia natural
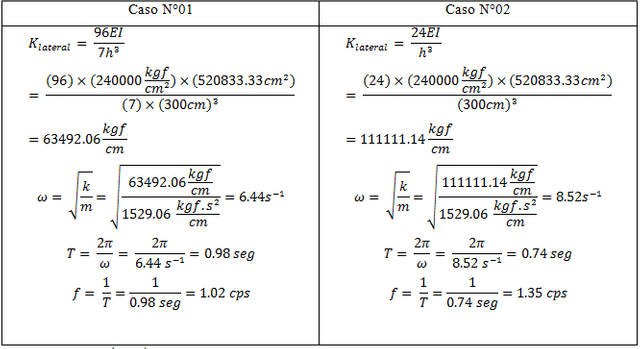
Fuente: Santana (2018)
CONCLUSIONES
1.-Al poseer el pórtico plano del caso N°=2 mayor rigidez, el valor del periodo natural (T) es menor al del caso N°01; lo que indica, que mientras tengamos sistemas estructurales más rígidos, los valores de período natural tenderán a disminuir. Este situación se extrapola a casos reales, por ejemplo, donde la estructura es muy flexible (valor de periodo alto), y se procede a aumentar su rigidez, colocando por ejemplo muros en lugares estratégicos de la misma.
2.- La frecuencia es inversamente proporcional al período, es decir, mientras el periodo aumenta la frecuencia disminuye; de allí a que la frecuencia del caso N°01 sea menor a la del caso N°02.
3.- El valor de periodo en las normas venezolanas de diseño sismoresistente es muy utilizado, por ejemplo en el desarrollo de métodos de análisis espectral, lo cual estaré abordando en próximas publicaciones.
4.- Una forma práctica de estimar aproximadamente el período natural en estructuras, es dividir el número de pisos de esta por diez. Aplicando esto al caso en estudio, nos daría un periodo natural aproximado de 0.1 segundos, el cual es un valor que sirve de referencia en los cálculos realizados.
FUENTES CONSULTADAS
1.- CHOPRA ANIL K.DINÁMICA DE ESTRUCTURAS. CUARTA EDICIÓN. PEARSON EDUCACION, MEXICO 2014.
2.- PAZ MARIO. DINÁMICA ESTRUCTURAL TEORIA Y CÁLCULO. EDITORIAL REVERTE ESPAÑA 1992.
3.- SANTANA ELÍAS. ESTUDIO DE LAS APLICACIONES DEL ANÁLISIS MATRICIAL EN LA OBTENCIÓN DE MATRIZ DE RIGIDEZ DE UN PÓRTICO PLANO. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/estudio-de-las-aplicaciones-del-analisis-matricial-en-la-obtencion-de-la-matriz-de-rigidez-de-un-portico-plano
Being A SteemStem Member
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Conozco algo del tema y mas que analizar tus conocimientos que son amplios, me agrada mas que no tienes problemas con dar este aporte y aquellos que trabajan con esos cálculos estructurales reciben un valioso beneficio de tu parte. Repito me agrada tu sencillez al presentar ese desarrollo estructural sin mezquindad. Un fuerte abrazo y sigue así que la vida se verá recompensada en tu caso. Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Los temas de estudio de la dinámica estructural en muchas ocasiones pueden resultar abstractos, es un reto darles ese toque didáctico. Gracias por tus buenos deseos. Saludos @profeyer!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Felicidades!

Únete a nuestro canal en discord y así puedes interactuar con toda la comunidad de habla hispana te esperamos!
https://discordapp.com/channels/354702649360121857/407281009130733578
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias @carloserp-2000, complacido por la invitación. Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Bien detallada y tecnica tu explicacion, tienes un nuevo seguidor!!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias @jmhb85, procurando detallar al máximo los temas estudiados, para que sean de utilidad a los amantes de la dinámica estructural. Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
bastante extenso pero bien explicado. saludos @eliaschess333.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias @atheneav, es un reto el abordaje didáctico de estos contenidos. Me complace tu opinión, saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
@eliaschess333 Gracias por compartir tus conocimientos con nuestra comunidad científica. Te felicito! Excelente post. Esperó tu próxima publicación.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias @joseleogon, encantado de compartir conocimientos en mis áreas de formación con la comunidad científica de STEEMIT, es un excelente camino para seguir creciendo. Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @eliaschess333, this post is the eighth most rewarded post (based on pending payouts) in the last 12 hours written by a Dust account holder (accounts that hold between 0 and 0.01 Mega Vests). The total number of posts by Dust account holders during this period was 11333 and the total pending payments to posts in this category was $4107.92. To see the full list of highest paid posts across all accounts categories, click here.
If you do not wish to receive these messages in future, please reply stop to this comment.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks @bitgeek, very interesting on the information presented; very useful to assess our growth in the scientific community of STEEMIT. Greetings!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
explicas con detalles en este post y lo cual hace que se entienda de forma mas fácil, tienes un seguidor mas.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Así es @aquiless, espero te sea de mucha utilidad. Me complace leer tu comentario. Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
@eliaschess333, muy bueno tu estudio. Una evidencia más de la exactitud de la matemática aplicada, por lo cual su aporte no solo permite la evolución del conocimiento, sino la solución de problemas reales.. excelente!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Sin lugar a dudas @mariselaestangab, el aporte de las matemáticas a la dinámica de estructuras es impresionante. Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Ojala hubiera leido hace 1 año hubiera podido sacar mas nota en ese bendito examen de ingenieria de control jejeje. Bueno por lo menos recorde lo tedioso que es menos mal que ya me gradue y que esa area no me llama la atencion. @andrysita
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit