INTRODUCCIÓN
En esta primera entrega desarrollaremos una visión matemática sobre un fenómeno que afecta a las edificaciones que se fundan sobre suelos arcillosos, sin las adecuadas previsiones desde el punto de vista geotécnico, y que trae como consecuencia asentamientos en las mismas; destacando que estos asentamientos, no se producen de forma instantánea, sino que ocurren tiempo después que la estructura ha sido fundada; de allí a que surja el término consolidación. Descubriremos los basamentos que rigen este fenómeno, basados en los principios de esfuerzos efectivos en la masa de un suelo y de permeabilidad de Darcy; para posteriormente con ayuda de las Matemáticas, llegar a expresiones generales, que nos permitan comprender el fenómeno de forma analítica. En la siguiente imagen, se presenta una visión global de los contenidos a estudiar.
Imagen N°01: una visión general de los contenidos a estudiar
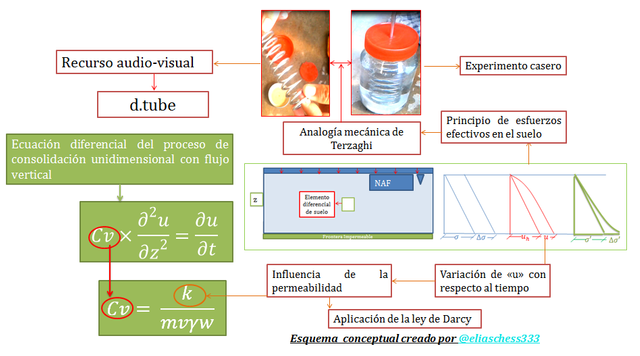
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. Las imágenes fueron capturadas con mi dispositivo Tablet VIT-T4000.
Con la intención de favorecer la comprensión didáctica del fenómeno de consolidación decidí preparar un recurso audio-visual, basado en la analogía mecánica de Terzaghi, representando las imágenes resaltadas en color “rojo” del esquema conceptual de la imagen N°01 parte de los contenidos a exponer en dicho video. En definitiva, este artículo constituye un esfuerzo del autor, para difundir conocimientos en el campo de la ingeniería geotécnica, e impulsar el desarrollo de un sentido crítico sobre los fenómenos que conlleva la interacción de nuestras estructuras con el suelo de fundación. Con mucho cariño para todos mis queridos lectores de esta plataforma de STEEMIT, espero disfruten del siguiente post:
DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR
El campo de acción del presente trabajo, lo estaremos contextualizando a los suelos de naturaleza arcillosa, que se encuentren en condición saturada. Al mismo tiempo, supondremos infinita la extensión horizontal del estrato en relación a su espesor (ver imagen N°03) por lo que se le da interés a las deformaciones que ocurran en sentido vertical; acotando que en esta misma dirección se desplaza el flujo, cuya expulsión es responsable de dichas deformaciones, dado que todos los vacíos están llenos de agua. También es importante resaltar que las partículas sólidas del suelo y el fluido en consideración (agua) se consideran incompresibles, es decir, la disminución del volumen del suelo (asentamiento) es consecuencia directa de la disminución de sus vacíos, y por ende de la expulsión del agua de los poros del mismo.
Todas estas hipótesis planteadas, en conjunto con los aportes de las Matemáticas, del principio de esfuerzos efectivos y la teoría de permeabilidad de Darcy, nos guían en el desarrollo de un planteamiento teórico – matemático, para dar con la ecuación diferencial del proceso de consolidación unidimensional con flujo vertical; cuyo surgimiento se remonta al mediados del siglo XIX a cargo de Terzaghi:
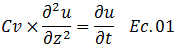
Esta ecuación, le da todo un basamento científico al estudio de los asentamientos diferidos en el tiempo (consolidación) que experimenta el suelo como consecuencia de la aplicación de una carga externa.
UNA VISIÓN CONCEPTUAL DEL FENÓMENO DE CONSOLIDACIÓN UNIDIMENSIONAL
Hacernos una idea conceptual de este fenómeno es clave a la hora de adentrarnos en los principios matemáticos que lo sustentan. Comencemos concibiendo al suelo, constituido por fases, como se ilustra en el esquema conceptual de la imagen N°02.
Imagen N°02: representación ideal de un suelo a través de un diagrama de fases
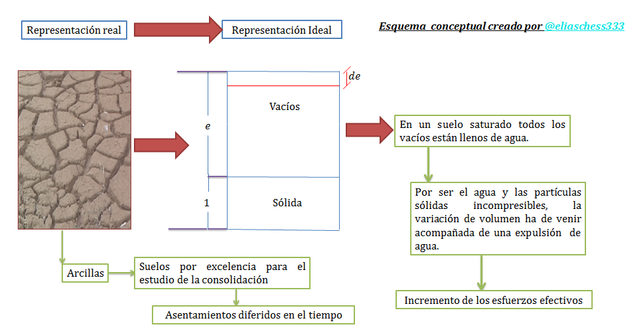
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. Las imágenes fueron capturadas con mi dispositivo Tablet VIT-T4000.
Dado que supondremos al suelo en condición saturada, sus vacíos están llenos de agua; por lo que una disminución de los mismos (asentamiento) se asocia con una expulsión del agua en cuestión, teniendo en cuenta que en el caso de las arcillas, por la baja permeabilidad, dicha expulsión es muy lenta, pudiendo tardar días, meses e incluso hasta años, de allí a que los asentamientos que se produzcan sean diferidos en el tiempo; hecho que describe el fenómeno de consolidación unidimensional; estas ideas se complementan de mejor manera desde la óptica de la teoría de esfuerzos efectivos.
Tenemos por lo tanto que los suelos en su condición natural presentan un estado de esfuerzos efectivos marcado por el espesor de los estratos “H” que origina una presión vertical “σ” y la presión hidrostática “uh” que depende en esencia de la posición del nivel freático (NAF), la cual para los fines de este artículo la estaremos considerando constante. La incorporación de una sobrecarga, producto de una acción del hombre, por ejemplo la construcción de una edificación, indudablemente originará una variación de los esfuerzos efectivos “σ’”, que comienza en primera instancia con el surgimiento de una presión en exceso a la hidrostática “u”; cuyo proceso de disipación en el caso de las arcillas ocurrirá diferido en el tiempo, tal como se señaló en el párrafo anterior. El siguiente esquema conceptual nos permitirá hacernos una mejor visión del cálculo de los esfuerzos efectivos “σ’” y la influencia de la sobrecarga “∆p”.
Imagen N°03: ilustración del cálculo de esfuerzos efectivos y el efecto de “∆p”
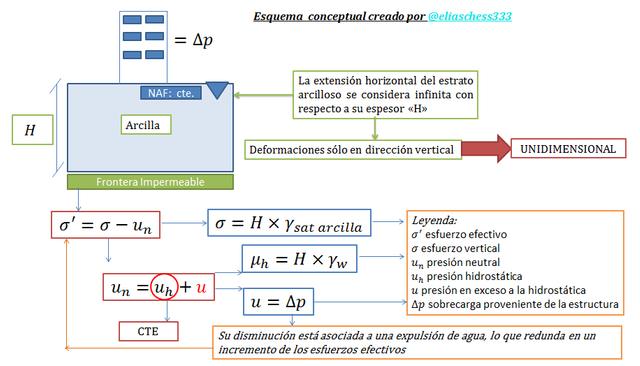
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
En la medida que “u” se vaya disipando, ocurrirá progresivamente una transferencia de esfuerzos a la estructura del suelo, directamente proporcional al aumento en los esfuerzos efectivos “σ’”, es decir, al contacto efectivo entre partículas, provocando una deformación. En la siguiente imagen se ilustra didácticamente este hecho:
Imagen N°04: variación de “u” con el tiempo y la profundidad “z”
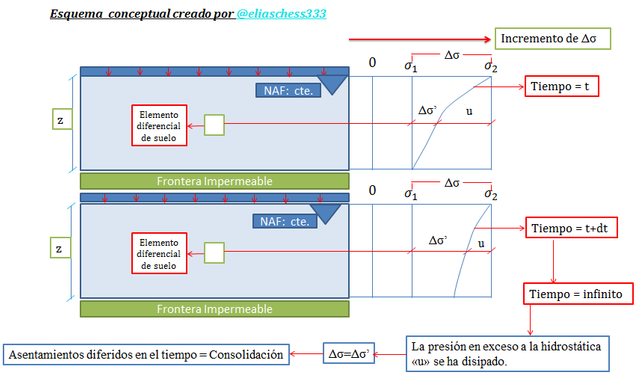
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
Para un tiempo idealizado como infinito, la presión en exceso a la hidrostática “u” se habrá disipado por completo, y el incremento de los esfuerzos efectivos “∆σ’” corresponderá directamente con el incremento de carga transmitido por la estructura, es decir:
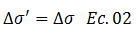
Para afianzar las ideas disertadas, comparto con ustedes el siguiente recurso audio-visual, en el cual tomo como referencia la analogía mecánica de Terzaghi, padre de la ciencia de la Mecánica de Suelos, a quien le debemos gran parte de los sustentos teóricos y matemáticos de este fenómeno que estamos estudiando. Disfruten del siguiente video:
Fuente: @eliaschess333, año: 2018. Nota: video elaborado por el autor con ayuda de las herramientas computacionales Camtasia Studio 8, Adobe Audition 3.0. Las capturas de video fueron realizadas con mi dispositivo Tablet VIT-T4000, y las mismas estuvieron a cargo de @monserratt3. Los esquemas conceptuales que se presentan fueron elaborados por el autor con las herramientas Microsoft PowerPoint y Paint.
▶️ DTube
▶️ IPFS
Todo lo anterior expuesto permite hacernos una idea matemática del fenómeno de consolidación unidimensional, atribuyéndolo a la variación con el tiempo “t” y la profundidad “z”, de la presión en exceso a la hidrostática “u”; por lo que rigurosamente la podemos expresar así:
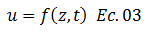
Dado que “u” es una función que depende de dos variables, esto abre las puertas a un tema de gran complejidad en las matemáticas, correspondiente a ecuaciones diferenciales en derivadas parciales; centrándonos en desarrollar en este artículo la ecuación que rige este fenómeno, de donde surgirán conceptos de importancia que nos permitirán comprenderlo en mayor medida.
LA CONSOLIDACIÓN UNIDIMENSIONAL DESDE UN ENFOQUE MATEMÁTICO. APLICACIÓN DE LA LEY DE DARCY
En los perfiles de suelo mostrados en la imagen N°04, se hizo alusión a un elemento diferencial de suelo; en el esquema conceptual de la imagen N°05 este elemento se presenta de forma ampliada, incorporando otros aspectos de importancia para lograr con las ideas de este tópico:
Imagen N°05: vista ampliada del elemento diferencial de suelo, aplicación de la ley de Darcy
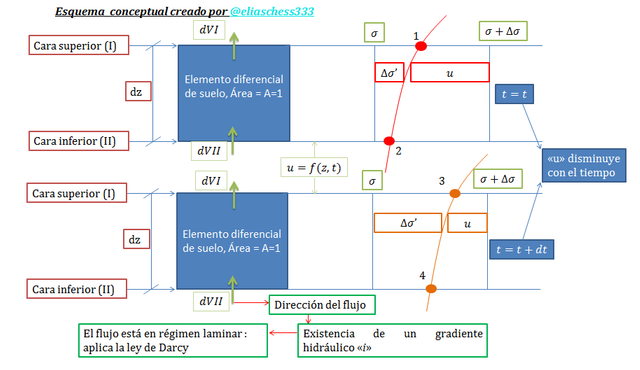
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
En primera instancia, analicemos de forma rigurosamente matemática la variación del exceso de presión a la hidrostática “u” con respecto a la profundidad “z” y el tiempo “t”. Tomando como referencia el punto 1 (ver imagen N°05), tenemos lo siguiente:
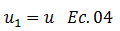
Este es el punto de partida en el tratamiento de esta variable, de allí a que no entre en juego ningún tipo de variación, expresada en términos de diferenciales. Al pasar al punto 2, obtenemos lo siguiente:
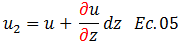
Notemos que comenzamos a utilizar el símbolo característico de derivada parcial, el cual se encuentra resaltado en color “rojo” en la ecuación N°05; debido a que “u” depende de dos variables. Destacando que para este caso en particular, su variación estará afectada por la profundidad “z”. Ahora bien, al tomar como referencia el punto 3 (ver imagen N°05) tenemos que:
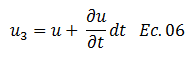
Una expresión totalmente lógica, puesto que “u1” y “u3” se encuentran en la misma profundidad, y lo que varía entre ellas es el tiempo “t”. Por su parte “u” en el punto 4, si involucra una variación influenciada por el tiempo “t” y la profundidad “z”, con respecto al punto 1, tomado inicialmente de referencia, por lo tanto:
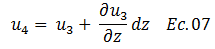
Sustituimos la ecuación N°06 en la N°07:
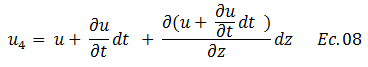
Rescribimos la ecuación:
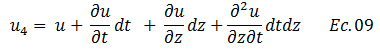
Comprendido el mecanismo de la variación de “u” para los puntos de referencia de la imagen N°05, surge el planteamiento de la siguiente interrogante:
¿Por qué hay movimiento del agua?
La existencia de flujo obedece a un gradiente hidráulico “i”, el cual hace alusión a la pérdida de carga por unidad de longitud.
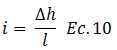
Dado que se está perdiendo la carga en exceso a la hidrostática “u”, conviene realizar el siguiente planteamiento:
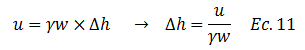
Expresando la longitud “l” en términos de “z”, y sustituyendo la ecuación N°11 en la N°10, se obtiene:
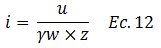
Al incluir en esta ecuación el término de derivadas parciales, obtenemos el gradiente hidráulico para el punto 1 (ver imagen N°05):
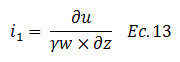
El gradiente hidráulico para el punto de referencia 2 es:
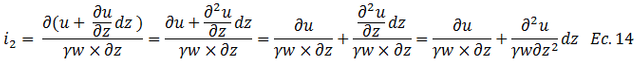
Dado que en la masa del suelo, el agua que es expulsada, producto de la aplicación de la carga externa sigue un régimen laminar, es aplicable la ley de Darcy, que en líneas generales establece que la velocidad que experimenta un fluido (agua) al atravesar un medio poroso (suelo), es directamente proporcional al gradiente hidráulico “i” y a la permeabilidad “k” de dicho medio. Por lo que:
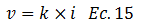
Basados en la ecuación N°15, el Volumen “V” del fluido que atraviesa el medio poroso, de área transversal unitaria “A=1” es:
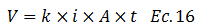
Dado que conocemos el gradiente hidráulico en los puntos de referencia 1 y 2; sustituyendo en la ecuación N°16 podemos obtener el volumen de agua que pasa por estos puntos de la siguiente manera:
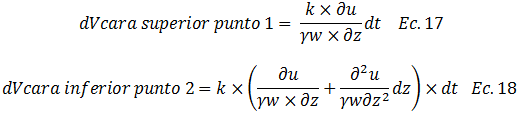
Rescribimos:
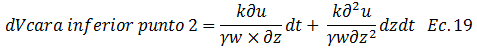
La variación de volumen “∆dV” es:
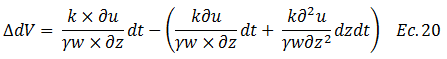
Por lo tanto:
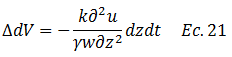
La ecuación N°21 la podemos interpretar como el agua neta que fue expulsada, lo que se traduce en una variación de volumen del suelo. El análisis que permitió llegar a la ecuación N°21, lo podemos también desarrollar tomando como referencia los puntos 3 y 4, y así darle mayor veracidad a dicha ecuación. Este proceso se ilustra en el esquema conceptual de la imagen N°06, donde para fines prácticos se plantea la siguiente nomenclatura:
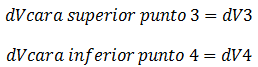
Imagen N°06: deducción de la expresión que representa la variación de volumen “∆V”
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.
Se tiene que despreciando los términos de orden superior, se llega a la misma expresión representada por la ecuación N°21, por lo que no hay dudas, que para las condiciones a las que se encuentra sometido el suelo, su asentamiento está asociado a una expulsión neta de agua; es interesante, proceder ahora a analizar este hecho desde la óptica del principio de esfuerzos efectivos.
LA CONSOLIDACIÓN UNIDIMENSIONAL DESDE UN ENFOQUE MATEMÁTICO. APLICACIÓN DEL PRINCIPIO DE ESFUERZOS EFECTIVOS
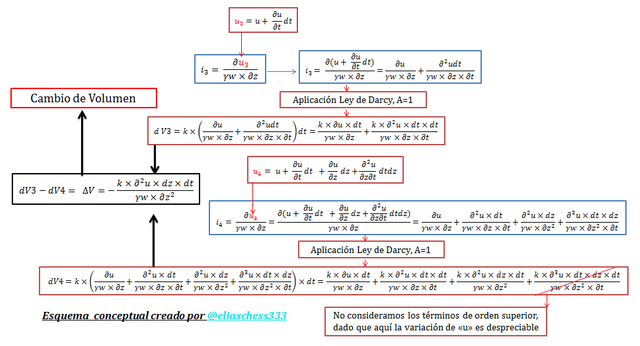
Es importante en los análisis que a continuación se presentan, tener presente las ideas expuestas en el esquema conceptual de la imagen N°07, en este orden de ideas la variación de volumen en un elemento diferencial de suelo “dz” y de área constante (unitaria), puede ser expresado por medio de la siguiente relación de proporcionalidad:
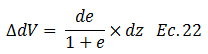
Imagen N°07: ilustración didáctica del proceso de obtención del coeficiente de compresibilidad
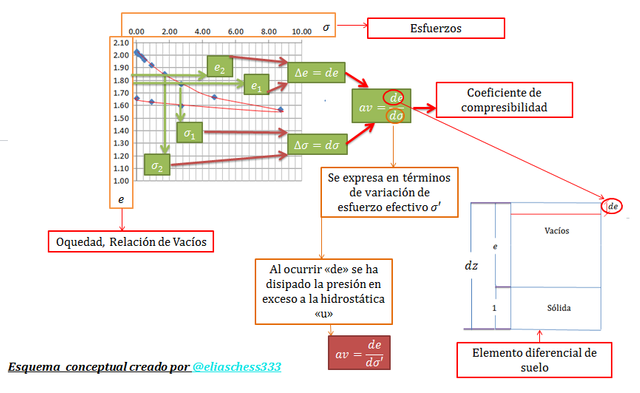
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint, Microsoft Excel y Paint.
Resulta evidente que si “de=0”, no habrá cambio de volumen. Ahora bien, partiendo de la expresión para el coeficiente de compresibilidad “av”, tenemos que:
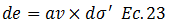
Procedemos a sustituir la ecuación N°23 en la N°22:
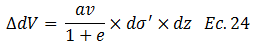
Es necesario reflexionar sobre lo que establece el principio de esfuerzos efectivo; por lo que te invito a revisar el esquema conceptual de la imagen N°03, a partir de allí, podemos definir la siguiente relación:
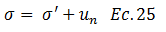
Se infiere que el esfuerzo vertical “σ” es constante en todo el tiempo; idea que queda respaldada por los gráficos presentados en los esquemas conceptuales de las imágenes N°04 y N°05; por lo que al expresar la ecuación N°25 en términos de diferencial se obtiene:
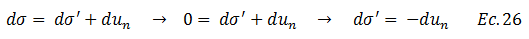
Adicionalmente la presión neutral “un” es la suma de la presión hidrostática “uh” y la presión en exceso a la hidrostática “u”, siendo la primera constante en el tiempo, puesto que depende de la altura del nivel freático, la cual para los fines de este trabajo no varía (ver imagen N°03), porque el estrato de suelo se considera siempre saturado; en este sentido:
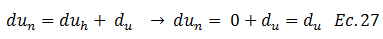
Basados en esta idea, la ecuación N°26 se rescribe así:
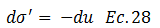
Esta ecuación en términos rigurosamente matemáticos, afirma las ideas que hemos expuesto, en cuanto al hecho de que la variación de los esfuerzos efectivos va en función de la variación de la presión en exceso a la hidrostática “u”. Procedamos a definir “du” dejando “z” constante y variando solo el tiempo “t”; para tal fin tomemos como referencia los puntos "1-3” y “2-4” del esquema conceptual de la imagen N°05, y las expresiones de “u” señalada a lo largo de las ecuaciones N°04, N°05, N°06 y N°09. Para los puntos “1-3” se tiene:
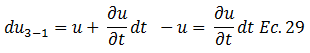
Por lo que:
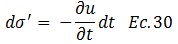
En lo que respecta a los puntos 4-2:
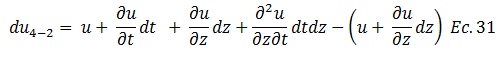
Rescribimos:
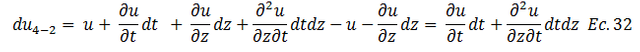
Despreciamos los términos de orden superior:
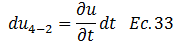
Por lo que:
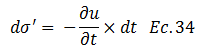
Se concluye que el incremento del esfuerzo efectivo “σ’” es el mismo en un determinado instante de tiempo “t” producto de la variación de la presión en exceso a la hidrostática “u”. Este hecho permite rescribir la ecuación N°24 de la siguiente manera:
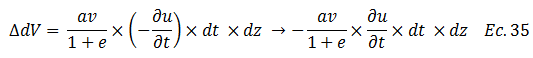
EN BÚSQUEDA DE LA ECUACIÓN DIFERENCIAL DEL PROCESO DE CONSOLIDACIÓN UNIDIMENSIONAL CON FLUJO VERTICAL
Procedemos a igualar las ecuaciones N°21 y N°35 de la siguiente forma:
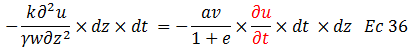
Cancelamos los términos semejantes:
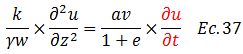
Despejamos el término resaltado en color “rojo”:
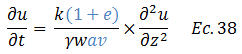
El término resaltado en color “azul” de la ecuación N°38 representa el inverso del coeficiente de variación volumétrica “mv”, el cual relaciona la compresibilidad del suelo con su volumen inicial:
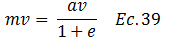
De allí a que la ecuación N°38 se pueda rescribir de la siguiente manera:
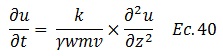
Finalmente vale la pena introducir el concepto de coeficiente de consolidación “Cv”:
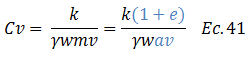
Por lo tanto:
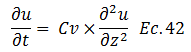
CONCLUSIONES
Las matemáticas nos sorprenden con la infinidad de aplicaciones que tienen, en todos los campos de la ingeniería, centrándonos en esta ocasión en el fenómeno de consolidación unidimensional de una arcilla. Entre las conclusiones de mayor relevancia tenemos:
1.- La variación de los esfuerzos efectivos “σ’” está directamente influencia por la disipación de la presión en exceso a la hidrostática “u”, condicionada esta última a la permeabilidad “k” del suelo.
2.- En el caso de las arcillas, esta permeabilidad es muy baja, por lo que la disipación de la presión en exceso a la hidrostática “u” ocurre diferida en el tiempo, fenómeno que se conoce como consolidación.
3.- El coeficiente de compresibilidad “av” no es una constante del suelo, dado que su variación está asociada a los incrementos de carga que este sufra.
4.- Un “av” alto indica que estamos en presencia de un suelo muy compresible.
5.- El coeficiente de consolidación “Cv” es de gran utilidad al momento de estudiar la evolución de los asentamientos en el tiempo.
En una próxima entrega, profundizaremos en la solución analítica de la ecuación diferencial de la ecuación N°42, lo cual permitirá llegar a expresiones de fácil uso en la rutina de un laboratorio de Mecánica de Suelos, cuando se desarrolla el ensayo de consolidación unidimensional; abriendo así las puertas a un abordaje experimental de este fenómeno.
FUENTES DE INFORMACIÓN CONSULTADAS
1.- BADILLO J. Y RODRÍGUEZ R. 2007. MECÁNICA DE SUELOS TOMO I. FUNDAMENTOS DE LA MECÁNICA DE SUELOS. EDITORIAL LIMUSA S.A. GRUPO NORIEGA EDITORES
2.- BADILLO J. Y RODRÍGUEZ R. 1995. MECÁNICA DE SUELOS TOMO III. FLUJO DE AGUA EN LOS SUELOS. EDITORIAL LIMUSA S.A. GRUPO NORIEGA EDITORES
LECTURAS RECOMENDADAS
3.- SANTANA E. 2018. ESTUDIO DEL FENÓMENO DE LICUEFACCIÓN DE SUELOS CON UN ENFOQUE CREATIVO AMPARADO EN EL PRINCIPIO DE ESFUERZOS EFECTIVOS. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/estudio-del-fenomeno-de-licuefaccion-de-suelos-con-un-enfoque-creativo-amparado-en-el-principio-de-esfuerzos-efectivos
Excelente trabajo elias fenomenal colocar un vídeo con un experimento didáctico explicando y simulando el enfoque de lo suelos con el resorte en una condición de saturacion
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias @gerardoalfred, me alegra que te haya gustado el recurso audio-visual, fue todo un reto lograrlo. La analogia mecánica de Terzaghi nos ayuda a comprender de un modo didáctico el fenómeno de consolidación. Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Magistral explicación @eliaschess333. Muy interesante la simulación de los suelos y su respuesta ante la aplicación de las cargas.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos @vjap55, eso que mencionas es uno de los princiaples retos de la ingeniería geotecnica, lo que lleva a formarnos un sentido critico sobre la interacción de nuestras estructuras con el suelo de fundación. Agradecido por tu comentario!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Buen trabajo @eliaschess333! Sin duda se nota tu compromiso en el estudio de estas temáticas, como se evidenció en el conversatorio semanal de #stem-espanol donde nos hablaste sobre sismoresistencia. Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias @eniolw, tanto la ingeniería geotecnica como la ingeniería sismoresistente representan campos de mucho estudio y dedicación. Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hi @eliaschess333!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Maravilloso post @eliaschess333. Estás como pez en el agua. Gracias por educarnos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Que grato leer su comentario @elvigia. Me llena de satisfacción poder compartir conocimientos en mis áreas de formación académica a través de STEEMIT. Gracias por el apoyo. Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
excelente post. upvoted follow Saludos desde Canada.
nos gustaría presentarte nuestro blog de noticias de Bitcoin y criptomonedas. Es hora de estar al día con la nueva economía mundial. Si te gusta nos puede seguirnos. gracias. https://steemit.com/@cryptonoticias
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Excelente post estimado @eliaschess333. Técnico pero también didactico, se nota tu dominio del tema. Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos @emiliomoron, me alegra que te haya gustado. Ese es el reto, hacer didáctica la gestión del conocimiento de estos temas de importancia en la ingeniería geotécnica. Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Trabajo bien contemplado... gracias por el aporte realizado....
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos @geovanny1000, agradecido por el apoyo!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
muy completo,, parece una tesis jeje... que importante esto.... que bueno compañero..
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias por el apoyo @cajalias7, saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos, no puedo darte un opinión objetiva ya que no es mi area de competancia. Muy complejos todo. Sinceramente te felicito por tus conocimientos y esfuerzo. Como es costumbre, esta vez estamos ante una siciliana variante dragoniana ;-)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias por estar al tanto de mis publicaciones. Saludos @soy-venezuelien!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Guao bastante complejo este tema pero puedo observar que lo dominas a la perfección
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Me complace leer tu comentario! Los temas asociados a la ingeniería geotecnica y sismoresistente me encantan, por lo que me esfuerzo mucho para avanzar en su comprensión. Saludos @anaestrada12!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
En mi ciudad natal (Maracaibo, Venezuela) construyeron hace décadas un conjunto residencial conformado por 4 torres de 10 pisos, al pasar del tiempo notaron que las paredes se empezaban a fisurar de forma diagonal, entonces cayeron en cuenta que fueron construidas en un terreno arcilloso. Al día de hoy han tenido que evacuar a todas las familias ya que existe peligro de derrumbe, dejando sin hogar a cientos de personas.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Tremenda experiencia @hgalue, lo presenciado fue un caso típico de falla por corte en las paredes; producto probablemente de asentamientos diferenciales, lo cual ocurre cuando la magnitud del asentamiento entre las bases de la estructura es distinta; originando una distorsión angular, que si excede los valores máximos permitidos, contribuye a la falla de los elementos estructurales, de allí la importancia de los estudios de suelos; a veces a estos no se les da la debida atención, y las consecuencias son lamentables y en este caso trascienden el tema material, dado que muchas personas han sido afectadas por este hecho. Si tienes fotografías de este caso, me gustaría verlas, me da curiosidad saber el tipo de sistema de fundación empleado. Saludos y gracias por compartirnos esta experiencia!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Amigo @eliaschess333, mis sinceras felicitaciones por este excelente trabajo, muy organizado, bien presentado y con un excelente contenido. Felicitaciones por el apoyo conseguido. Estaré esperando la siguiente parte. Saludos cordiales.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Amigo @tsoldovieri que alegría ver tu comentario. Trabajando fuerte en la parte II de este post. Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit