¿Qué es GeoGebra?
Interfaz y opciones.
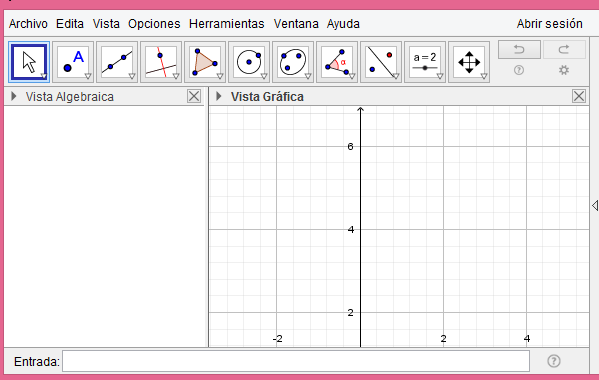
La verdad es que la interfaz de Geogebra es bastante amigable y sencilla de usar en la parte de arriba vemos una serie de ventanas las cuales dejare que sean ustedes mismos quienes las exploren, encontraran una serie de opciones relacionadas sobre todo con la configuración de la vista gráfica.
Con lo que trabajaremos normalmente es con la barra de herramientas en ella encontramos todas las opciones para realizar nuestras simulaciones.
Barra de herramientas:

En la primera ventana encontramos opciones de arrastre que podemos realizar con el cursor:
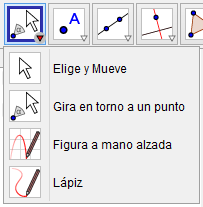
En la segunda ventana encontramos opciones para crear puntos y otras relacionadas con esto:
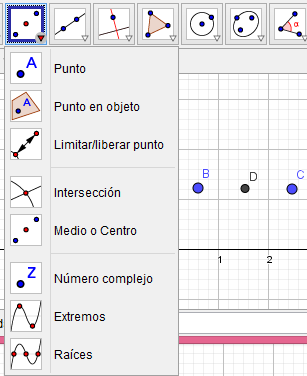
La primera opción nos permite crear puntos sobre cualquier parte de la vista gráfica y con medio o centro podemos crear un punto justo en el centro de otros dos, podemos ver en la imagen dos puntos B y C, el punto D es el resultado de usar la opcion medio o centro solo basta seleccionar esta opción y hacer click sobre los dos puntos de los cuales queremos obtener el punto central.
En la tercera ventana encontramos opciones para crear segmentos de linea y vectores:
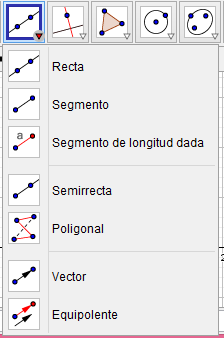
Si seleccionamos una de las opciones y dejamos el cursor sobre ella nos aparece una pequeña descripción sobre como funciona la opción, esto nos puede dar una idea de como usarla sin embargo interactuar con ella es la mejor forma de aprender.
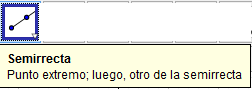
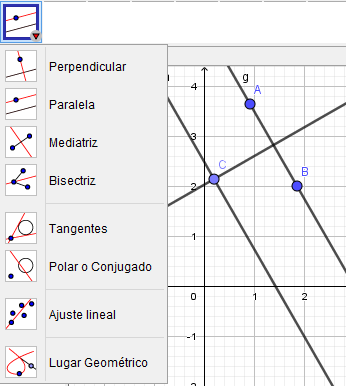
En la cuarta ventana encontramos opciones de tipos de rectas a un punto u otras rectas:
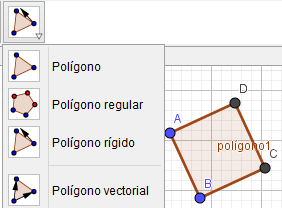
En la quinta ventana encontramos opciones para crear poligonos:
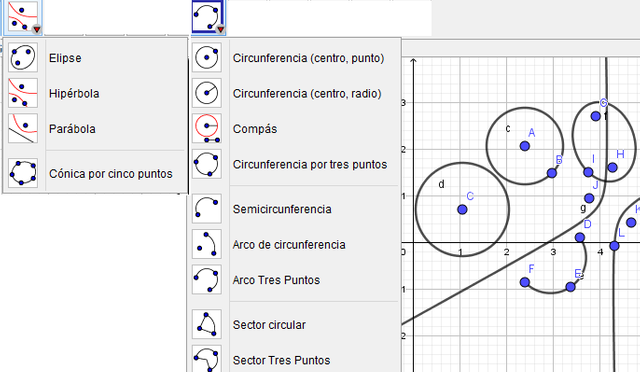
En las siguientes dos ventanas encontramos opciones para crear cónicas:
En la octava venta encontramos opciones para reflejar objetos, rotarlos y trasladarlos:
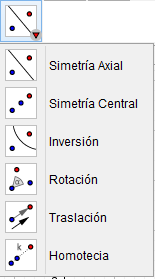
Llegamos a la penúltima ventana:
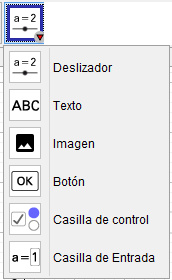
En esta ventana encontramos la opción mas importante a la hora de crear nuestras animaciones si bien todas las anteriores no permiten crear la estructura de estas la opción de deslizador nos permite darle movimiento a nuestros objetos, ya que permite ajustar el valor de un numero lo cual usaremos para cambiar las coordenadas de nuestros puntos. Para hacer uso de esta opción solo basta seleccionarla y hacer click sobre cualquier zona libre de la vista gráfica al hacerlo se abrirá la siguiente ventana con todas las opciones de configuración de nuestro deslizador:
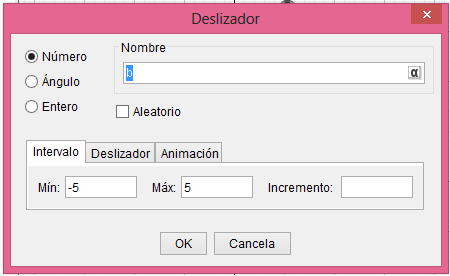
En la primera ventana podemos configurar la variación de nuestro deslizador y controlar el incremento de este, en las siguientes dos encontramos opciones sobre la orientación del deslizador y la forma de repetición.
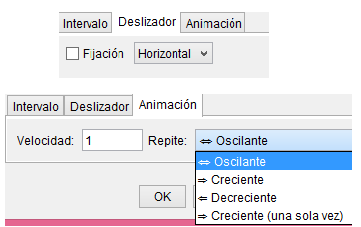
Ejemplos deslizadores:


Podemos ver que los resultados son bastante intuitivos para los otros dos tipos de repeticion ya sabemos que esperar, algo muy importante es que al crear cualquier objeto sobre nuestra vista grafica y hacer click derecho sobre el se nos despliega una ventana con una serie de opciones:

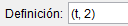
Al hacer click en propiedades se abre la ventana de preferencias de nuestro objeto en ella podemos configurarlo, cambiar su nombre, color, tamaño, forma, entre otras cosas; lo mas importante aqui es la casilla de definición en esta casilla podemos configurar las coordenadas de nuestro punto:
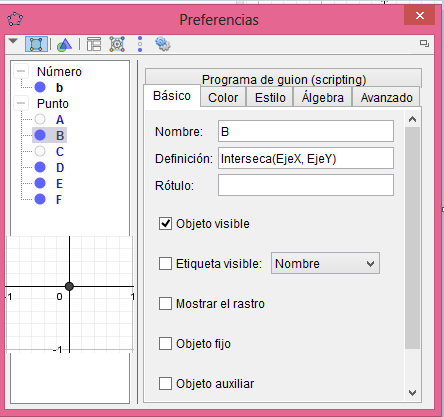
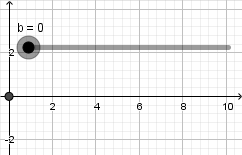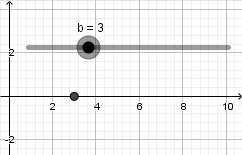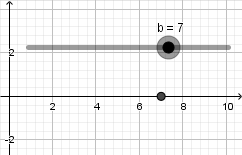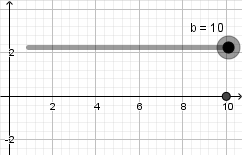
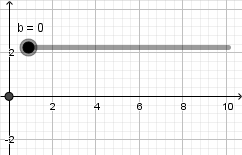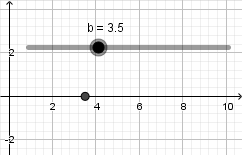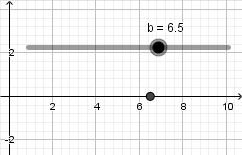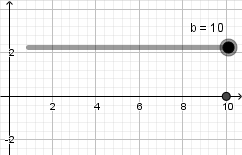
Crearemos un punto, daremos click derecho sobre el y entraremos en propiedades para abrir la ventana de preferencias, para escribir las coordenadas de nuestro punto debemos abrir un parentesis y escribir el primer valor el cual corresponde a la coordenada en el eje x luego una coma e introducimos el siguiente valor correspondiente a la coordenada en el eje y, en este ejemplo queremos un punto que se mueva solamente sobre el eje x por lo tanto escribimos su definición de la siguiente forma haciendo uso del deslizador "b" que antes creamos:  hacemos la coordenada y = 0 para limitar al punto a estar sobre el eje x el resultado es el siguiente:
hacemos la coordenada y = 0 para limitar al punto a estar sobre el eje x el resultado es el siguiente:
<
Simulación Movimiento rectilíneo uniforme:
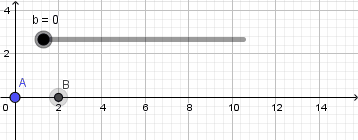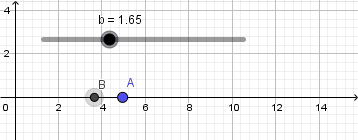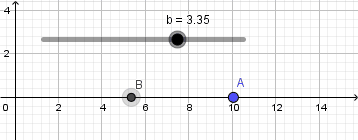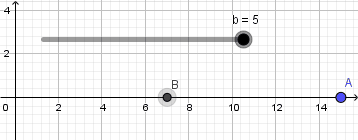
Para este ejemplo crearemos dos puntos y en sus definiciones tendremos para el punto "A"  y para el punto "B"
y para el punto "B"  estos valores que he puesto para la coordena x de los puntos no son mas que la ecuación de movimiento para un movimiento rectilíneo, para el punto "A" establecí que su posición inicial es 0 y su velocidad de 3 metros por segundo siendo "b" el valor del tiempo el cual esta dado por nuestro deslizador, para el punto "B" establecí una posición inicial de 1 metro y velocidad de 1 metro por segundo. Obtenemos como resultado la siguiente pequeña y sencilla simulación:
estos valores que he puesto para la coordena x de los puntos no son mas que la ecuación de movimiento para un movimiento rectilíneo, para el punto "A" establecí que su posición inicial es 0 y su velocidad de 3 metros por segundo siendo "b" el valor del tiempo el cual esta dado por nuestro deslizador, para el punto "B" establecí una posición inicial de 1 metro y velocidad de 1 metro por segundo. Obtenemos como resultado la siguiente pequeña y sencilla simulación:

Mi primera animación.

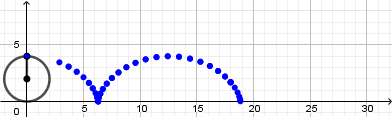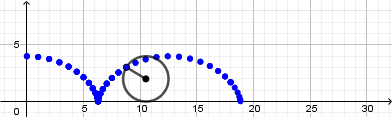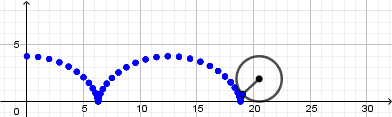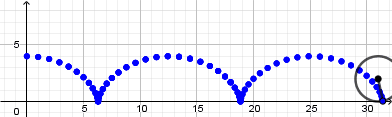
Como ya les dije conocer bien nuestro fenómeno es vital para poder realizar nuestras animaciones ya que al saber las ecuaciones que lo rigen podemos escribirlas en la barra de entrada y obtendremos el fenómeno. En el caso de la cicloide al saber sus ecuaciones parametricas podemos escribirlas en la barra de entrada de la siguiente forma:
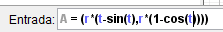
Al presionar enter automáticamente se nos creará un punto que tendrá por definición las ecuaciones parametricas de la cicloide, ademas de esto al no tener definido que es "r" y "t" se nos crearan dos deslizadores para estas variables lo cual es conveniente ya que nuestra cicloide ira formándose a medida que avance el tiempo.
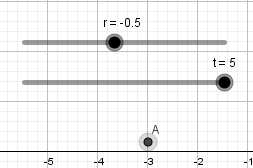
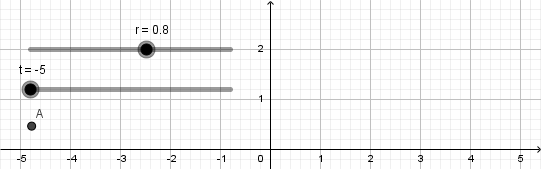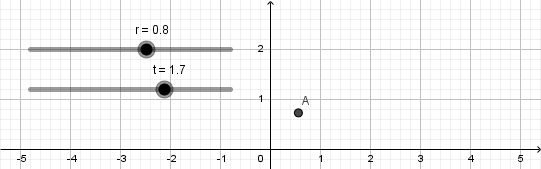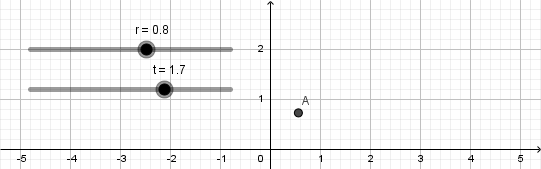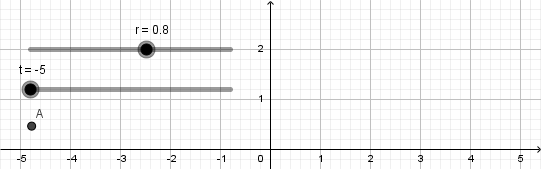
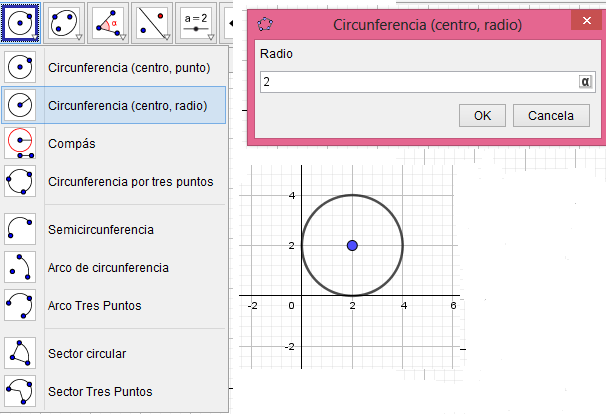
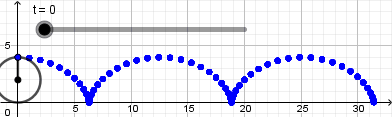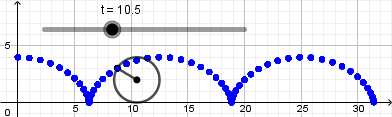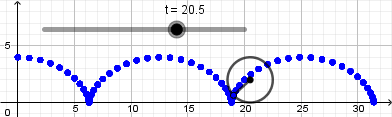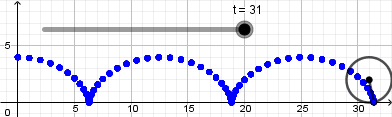
Esto nos da como resultado lo siguiente:
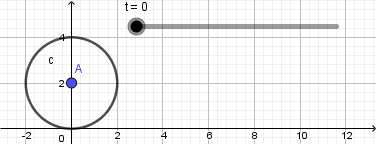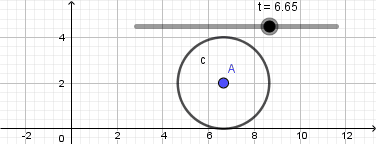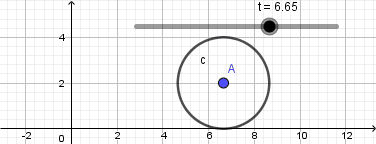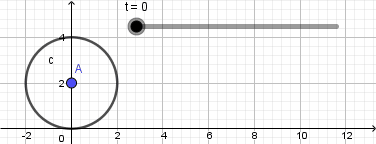
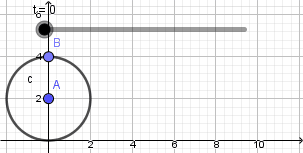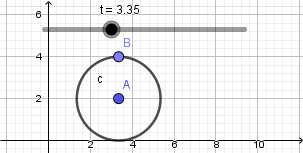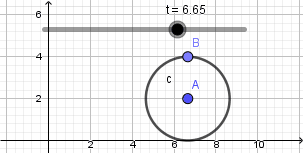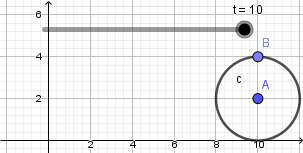
Como vemos el punto no se mueve de su posición la razón es que nuestra circunferencia en realidad no está "rodando" para resolver esto y crear el efecto de que la circunferencia está rodando usaremos la opción "rotacion" ubicada en la novena ventana de la barra de herramientas y la aplicaremos sobre el punto que creamos sobre la circunferencia, al seleccionar esta opción haremos click sobre el punto y luego sobre el punto central de la circunferencia que será el centro de rotación, al hacerlo se abrirá una ventana donde nos pedirá ingresar el ángulo de rotación y acá escribiremos:
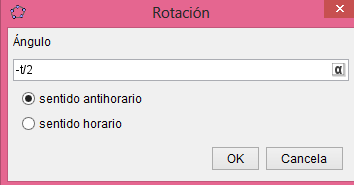
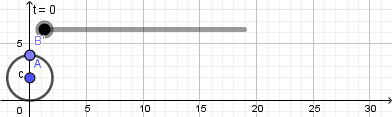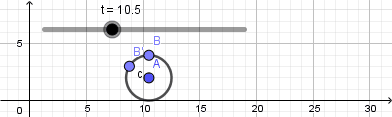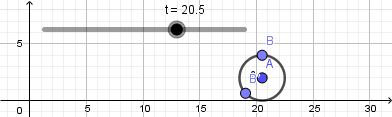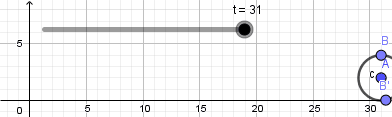
Pueden seguir agregando más detalles explorando las preferencias de los objetos creados, cambiar sus colores, tamaños, estilo de línea entre otras cosas, luego de que hayan agregado todas los detalles que deseen hay que proceder a crear la animación como tal ya que todo lo que hemos hecho esta en un archivo en formato .ggb pero como mencioné anteriormente GeoGebra nos permite exportar la vista gráfica a diferentes formatos entre ellos como una animación .gif, para hacer esto hacemos click en archivo seleccionamos exportar y luego Vista gráfica a GIF animado se abrirá una ventana donde en el caso de tener varios deslizadores debemos seleccionar el que le da movimiento a todo lo que hemos creado después de hacer esto damos click en exportar, seleccionamos la dirección donde guardaremos la animación y listo, esperamos que se cree el archivo .gif y tendremos nuestra animación lista para ser usada.
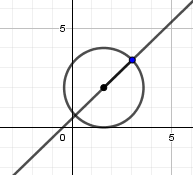
Luego de esto crearemos un punto sobre la recta dentro de la circunferencia y otro sobre la recta fuera de la circunferencia:
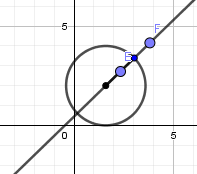
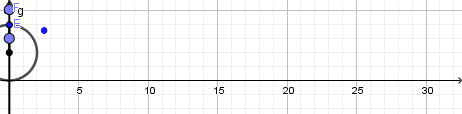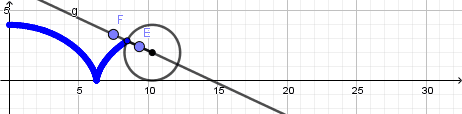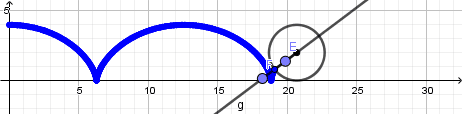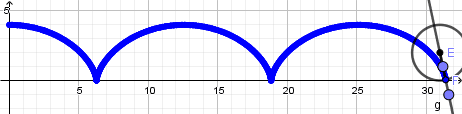
Los puntos dentro y fuera de la circunferencia describen una cicloide acortada y alargada respectivamente, de igual forma activamos el rastro para cada uno de estos puntos y ocultamos la recta dando click derecho en ella y desmarcando la opción de objeto visible cambiamos los colores, tamaño y estilo de los puntos a nuestro gusto y obtenemos lo siguiente:
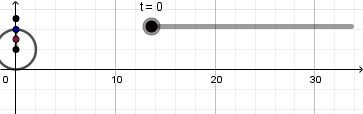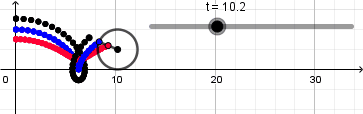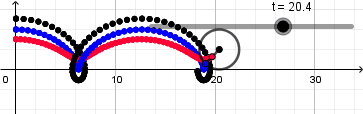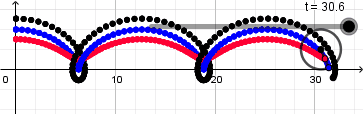
Desde este link https://www.geogebra.org/material/download/format/file/id/haycannc pueden descargar el archivo .ggb de la animación y guiarse aún más.
Y desde aqui pueden interactuar con la animación desde la página de GeoGebra.

Espero se hayan motivado y empiecen a explorar este increíble software para crear por ustedes mismos sus animaciones solo deben dar rienda suelta a su creatividad e imaginación.
Para leer contenido de calidad sobre ciencia los invito a visitar la etiqueta #stem-espanol.
Cualquier duda y sugerencia les agradecería que me la hicieran saber en los comentarios.
Gracias @luiscd8a, tomaré tu post sobre GeoGebra, como herramienta para diagramar mis artículos, y poder presentar imágenes GIF en mis manuscritos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Éxito en la tarea de elaborar tus animaciones cualquier inquietud no dudes en preguntar.
Saludos @lupafilotaxia.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Excelente post estimado @luiscd8a. Espero poder aprender de este maravilloso mundo. Aunque usted lo explicó muy bien. Ya guardé su post en favoritos para cuando lo necesite acceder a el. Felicitaciones es un gran aporte a la comunidad. Especialmente a nosotros los físicos que necesitamos de la matemática visual.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muchas gracias por tan buen comentario @djredimi2, es gratificante poder aportar algo mas que ayude a la comunidad. Próximamente vendrá otra publicación donde se pondrán en uso otras herramientas del software, cualquier duda que te surja sobre su uso no dudes en preguntar.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos. Muy lindo tu post. Aunque no es mi área, lo estético siempre capta mi atención.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muchas gracias por su comentario @elvigia, me alegra saber que mediante las animaciones puedo llamar la atención de personas que no estén tan familiarizadas con el área.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Excelente @luiscd8a. No soy muy bueno manejando ese tipo de programa pero con tu post voy a intentarlo. Gracias y saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
En la practica está la clave, próximamente exploraremos otras herramientas del software. Saludos @josedelacruz
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Excelente tutorial, que despierta el interés de seguir profundizando en este interesante programa "GeoGebra Classic 5". Tengo como tarea descargarlo y comenzar a practicar. Gracias por compartir tus conocimientos. Saludos @luiscd8a!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias por tu comentario @eliaschess333 así es hay que practicar, pronto vendrán otros artículos explicando diferentes herramientas.
Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hi @luiscd8a!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Felicitaciones @luiscd8a. El artículo está muy bien hecho y el contenido puede ser de mucha utilidad. Una sugerencia, dado que Geogebra tiene licencia GPL, sería más justo referirse a él como "software libre" o FLOSS, en lugar de sólo "código abierto" ;-)
Espero seguir leyendo tus posts, en especial sobre este tipo de contenidos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muchas gracias @eniolw tendré en cuenta tu sugerencia, pronto vendrán mas artículos sobre este software!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muy buena herramienta @luiscd8a, es muy ilustrativa y detallada tu explicación, intentare usarla, experimentando con varios fenómenos
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias por tu comentario @joseg, excelente, cualquier inquietud no dudes en preguntar.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit