En el presente artículo se abordará el concepto matemático del factorial de un numero y se explicará un método para aproximar su valor. El factorial de un número entero positivo n se define como el producto de todos los números enteros positivos menores o iguales que n, por ejemplo
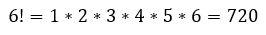
En el caso del número cero por definición se asume 0!=1. A continuación se muestran los primeros 10 números factoriales
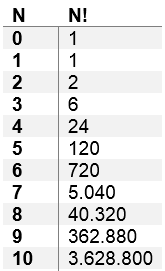
Tabla N° 1 Ejemplos de factoriales --- Fuente: Elaboración propia
La función factorial se usa en numerosas áreas de la matemática, tales como la estadística y combinatoria, sin embargo, para números enteros grandes es muy complicado calcular el factorial debido al elevado número de operaciones que implica, por esta razón se suele usar una aproximación muy famosa conocida como la fórmula de Stirling
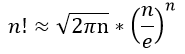
Esta fórmula de aproximación arroja valores bastante cercanos a la función factorial tal como se puede apreciar en la siguiente tabla
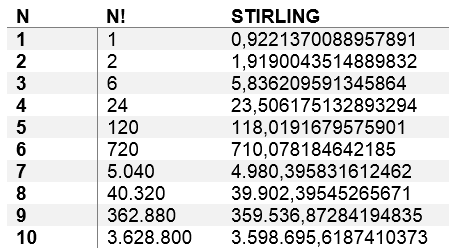
Tabla N° 2 Valores de la fórmula de Stirling para los primeros diez números enteros --- Fuente: Elaboración propia
Ahora se estudiará el comportamiento del error porcentual al aplicar la fórmula de Stirling para distintos valores de n, la fórmula para el error porcentual es la siguiente

El siguiente código en java permite evaluar el error porcentual entre la función factorial y la aproximación de Stirling para diferentes valores de n
public static void main(String[] args) {
for (int i = 1; i < 150; i++) {
Double f = factorial(i).doubleValue();
Double st = stirling(i);
Double ep = Math.abs(100 * (st - f) / f);
System.out.println(i + " " + ep + "%");
}
}
public static BigInteger factorial(int n) {
BigInteger res = BigInteger.ONE;
for (int i = 1; i <= n; i++) {
res = res.multiply(new BigInteger(Integer.toString(i)));
}
return res;
}
public static Double stirling(int n) {
Double res = Math.sqrt(2 * Math.PI * n) * Math.pow(n / Math.E, n);
return res;
}
Obteniendo los siguientes resultados
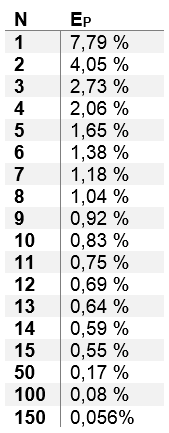
Tabla N° 3 Error porcentual entre la función factorial y la fórmula de Stirling para distintos valores de n --- Fuente: Elaboración propia
Como se puede observar en la tabla N° 3 el error de la aproximación tiende a decrecer a medida que n aumenta, por lo tanto la aproximación de Stirling es bastante adecuada para estimar factoriales de números grandes. Este resultado coincide con el límite que origina la fórmula de Stirling el cual es
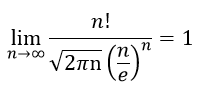
Por razones obvias para que este límite tienda a uno tanto el numerador como el denominador deben tener valores muy cercanos, de este hecho se obtiene la fórmula de Stirling para aproximar el factorial de un número.
Muy interesante @ydavgonzalez :)
Increíble que aparezca tanto pi como e en la fórmula.
¿Se ha demostrado que dicho límite tiende a 1? Un saludo
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Si, está demostrado, aquí puedes ver la demostración
http://fernandorevilla.es/blog/2017/04/06/formula-de-stirling-demostracion/
Saludos desde Venezuela
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Amo profundamente las publicaciones que hablan de las ciencias puras! Considero que la fobia a las matemáticas se dan por la deficiencia en pedagogía de los facilitadores.
Nota: Voto :*
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit