
Fuente: Elaboración propia utilizando Microsoft Office 2010.
Un gran saludo a toda la comunidad de Steemit y a los miembros de #STEM-ESPANOL y #STEEMSTEM, después de un receso forzado debido a cambios en mi vida personal y laboral estoy retomando la publicación de artículos científicos en Steemit, en el artículo de hoy abordaré una de las aplicaciones de los límites y derivadas de funciones de una variable, específicamente la relacionada con la definición de la derivada como razón de cambio de dos variables.
En diversos cursos de cálculo al introducir el concepto de derivada se suelen emplear dos enfoques, conocidos popularmente como “sentido geométrico” y “sentido físico” del concepto de derivada, el sentido geométrico se basa en la definición de derivada como pendiente de la recta tangente a la función original en un punto dado, mientras que el sentido físico hace referencia a la derivada de la función posición como el equivalente a la velocidad instantánea de la partícula en un tiempo dado, de esta forma al hablar de velocidad instantánea se hace alusión a la razón a la que cambia la posición de la partícula en función del tiempo.
Es decir, se crea una asociación entre el concepto de derivada y la razón de cambio de una variable respecto a otra, en este sentido la notación:
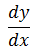
Que se usa para representar a la derivada, en muchos problemas suele ser tratada como la razón a la que cambia la variable y en función del cambio en la variable x, es decir, si por cada aumento de una unidad en x la variable y aumenta dos unidades, se puede establecer que
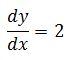
Un ejemplo claro del uso de la derivada como razón de cambio, lo tenemos a continuación:
Ejemplo N° 1
La ganancia de una empresa depende de su producción, por cada unidad de producto que se elabore la empresa gana 1.000 Bs. S., represente esta relación utilizando la notación de derivada como razón de cambio.
Se establece la variable x como el número de unidades producidas y la variable y como la ganancia de la empresa en Bs. S., teniendo esto en cuenta se cumple que

Ahora para encontrar la función de ganancia se encuentra la antiderivada de esta expresión en función de la variable x, obteniendo
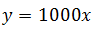
Esta función permite calcular la ganancia obtenida (Bs. S), en base a la producción (unidades de producto), sin embargo, en la práctica los problemas de razones de cambio suelen emplear variables que se relacionan entre si como se apreciará en el siguiente ejemplo:
Ejemplo N° 2
Un hombre corre a velocidad constante de 3 m/s y atraviesa un punto determinado en dirección al este, 15 minutos después otro hombre atraviesa el mismo punto en dirección al norte corriendo a una velocidad de 2,5 m/s. ¿Qué tan rápido cambia la distancia entre ambos hombres 10 minutos después de que el segundo hombre atraviesa el punto? ¿A que valor tiende la razón de cambio de la distancia entre ambos corredores asumiendo que los dos hombres nunca se detienen?
Para resolver este problema se representará el movimiento de ambos hombres en el plano cartesiano, estableciendo en el origen el punto por el que pasan ambos corredores.
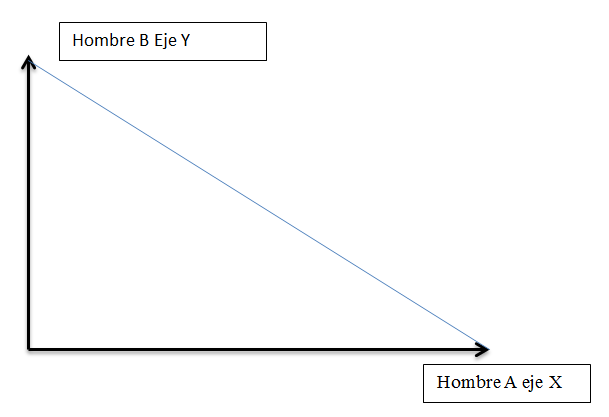
Imagen N° 1 Representación en el plano cartesiano del recorrido de los dos corredores. Fuente: Elaboración propia.
Sea t el tiempo en segundos desde el instante en que el segundo hombre atraviesa el punto dado, llamemos al primer hombre A y al segundo B, se cumple que los hombres A y B están en las coordenadas X y Y respectivamente, como la velocidad de los corredores por definición es la razón de cambio entre la distancia recorrida y el tiempo, para el primer corredor
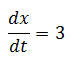
y para el segundo corredor se cumple
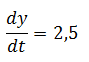
Representando por z la distancia entre ambos corredores se desea encontrar el valor de
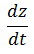
En el instante de tiempo t=600 segundos (10 minutos), en la imagen número 1 apreciamos que la distancia entre ambos corredores se puede modelar mediante el teorema de pitágoras
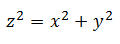
Derivando en función de t
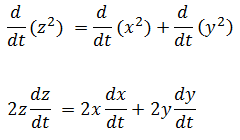
Sustituyendo las velocidades de ambos corredores
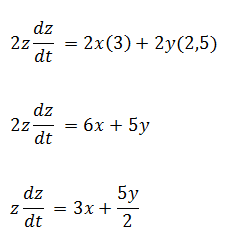
Por la forma en que hemos planteado el problema se cumple que la variable x y la variable y representan las distancias recorridas por ambos corredores, teniendo en cuenta que el tiempo t comienza a correr una vez que el segundo corredor cruza el punto dado, se cumple que el primer corredor ya tiene 15 minutos de recorrido, es decir, se obtienen los siguientes valores para ambos corredores
| Corredor | Velocidad | Tiempo corriendo en t=600 seg | Distancia recorrida |
|---|---|---|---|
| A | 3 m/s | 25 min (1.500 seg) | 4.500 m |
| B | 2,5 m/s | 10 min (600 seg) | 1.500 m |
Tabla N° 1. Velocidad, tiempo y distancia del recorrido de ambos corredores. Fuente: Elaboración propia.
La distancia entre ambos corredores es de
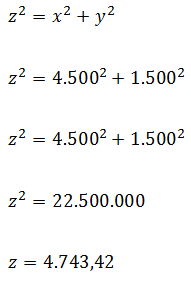
Luego al sustituir los valores de las distancias
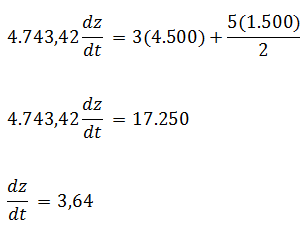
Es decir, 10 minutos después de que el segundo hombre atraviesa el punto dado, la razón de cambio de la distancia que separa a ambos corredores es de 3,64 m/s.
El resultado obtenido anteriormente puede ser verificado utilizando el Sistema de Álgebra Computacional Maxima y el siguiente Script
/*******************************+/
/ DERIVADA COMO RAZÓN DE CAMBIO /
/ Licdo Ysmael González /
/*********************************/
t:0$
while t<=600 do
(
x:3(t+900),
y:2.5t,
z:sqrt(xx+yy),
razon:(3x+5*y/2)/z,
print("Tiempo: ",t," Razón_de_cambio: ",razon),
t:t+60
);
Con este script se puede observar el valor de la razón de cambio en cada minuto transcurrido, obteniendo los siguientes resultados:
"Tiempo: "0" Razón_de_cambio: "3
"Tiempo: "60" Razón_de_cambio: "3.125971334811328
"Tiempo: "120" Razón_de_cambio: "3.229614135438366
"Tiempo: "180" Razón_de_cambio: "3.315397747719974
"Tiempo: "240" Razón_de_cambio: "3.386869768959255
"Tiempo: "300" Razón_de_cambio: "3.446826894492818
"Tiempo: "360" Razón_de_cambio: "3.4974699623212
"Tiempo: "420" Razón_de_cambio: "3.540533467151972
"Tiempo: "480" Razón_de_cambio: "3.577389218604988
"Tiempo: "540" Razón_de_cambio: "3.609127416944956
"Tiempo: "600" Razón_de_cambio: "3.636619309193636
Lo cual coincide con el valor obtenido de forma analítica, ahora para determinar la razón de cambio de la distancia entre ambos corredores si los dos corren de forma indefinida se debe recordar que
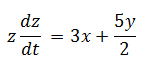
Luego
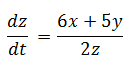
Ahora recordando el teorema de pitágoras y combinándolo con la expresión anterior
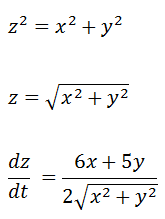
Teniendo en cuenta que los valores de las distancias están en función del tiempo de acuerdo a las siguientes relaciones
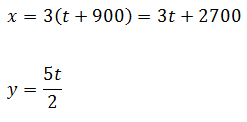
Al combinar estas expresiones con la razón de cambio de z en función del tiempo t se obtiene
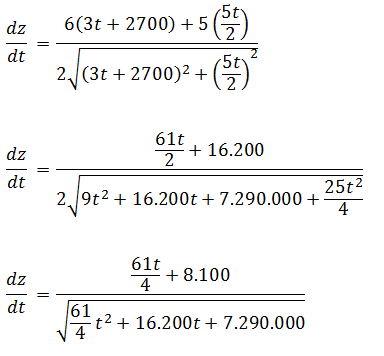
Si ambos corredores nunca se detienen entonces el tiempo tiende a infinito, es decir, la razón de cambio se expresa usando el concepto de límite
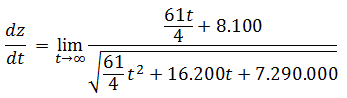
Este límite puede resolverse dividiendo tanto el numerador como el denominador entre t
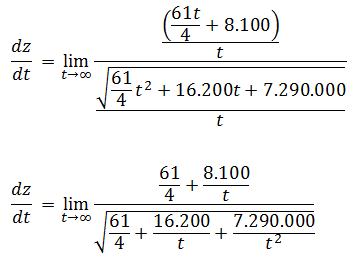
Como se trata de un límite y t tiende a infinito, los cocientes en los que t aparezca en el denominador tienden a cero, es decir
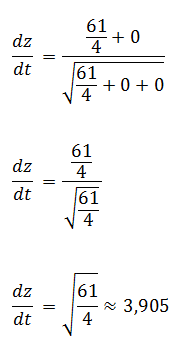
Es decir, si ambos corredores nunca se detienen la razón de cambio de la distancia que los separa tenderá al valor de
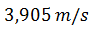
Este resultado puede ser verificado utilizando Maxima y el siguiente Script
/*******************************+/
/ DERIVADA COMO RAZÓN DE CAMBIO /
/ Licdo Ysmael González /
/ STEM-ESPANOL /
/ UNEFM 2016 /
/*********************************/
t:0$
while t<=90000 do
(
x:3(t+900),
y:2.5t,
z:sqrt(xx+yy),
razon:(3x+5*y/2)/z,
print("Tiempo: ",t," Razón_de_cambio: ",razon),
t:t+6000
);
Obteniendo los siguientes resultados:
"Tiempo: "0" Razón_de_cambio: "3
"Tiempo: "6000" Razón_de_cambio: "3.896187649304796
"Tiempo: "12000" Razón_de_cambio: "3.90269103759635
"Tiempo: "18000" Razón_de_cambio: "3.90401135806198
"Tiempo: "24000" Razón_de_cambio: "3.904489315309311
"Tiempo: "30000" Razón_de_cambio: "3.904714522308228
"Tiempo: "36000" Razón_de_cambio: "3.904838223332682
"Tiempo: "42000" Razón_de_cambio: "3.904913380349162
"Tiempo: "48000" Razón_de_cambio: "3.904962431018241
"Tiempo: "54000" Razón_de_cambio: "3.904996202094189
"Tiempo: "60000" Razón_de_cambio: "3.905020438661182
"Tiempo: "66000" Razón_de_cambio: "3.905038419131819
"Tiempo: "72000" Razón_de_cambio: "3.905052125038026
"Tiempo: "78000" Razón_de_cambio: "3.905062811271336
"Tiempo: "84000" Razón_de_cambio: "3.905071303875673
"Tiempo: "90000" Razón_de_cambio: "3.905078164606112
El cual es el mismo resultado obtenido al resolver el límite, poniendo de relieve la eficacia del modelo matemático utilizado.
CONCLUSIONES
Los límites y derivadas de funciones de una variable tienen una gran cantidad de aplicaciones prácticas en la vida cotidiana.
Para obtener resultados acordes a la realidad en problemas de razones de cambio relacionadas es importante prestar mucha atención a la fase del modelado matemático.
Los Sistemas de Álgebra Computacional permiten verificar los resultados obtenidos mediante el análisis matemático, incluso permiten conjeturar los valores a los que tienden los límites al infinito.
REFERENCIAS BIBLIOGRÁFICAS Y LECTURAS RECOMENDADAS
Anton, Bivens y Davis (2010), Cálculo de una variable, Trascendentes tempranas. 2da edición Editorial Limusa Willey.
Budnick (2007), Matemáticas aplicadas para administración, economía y ciencias sociales. 4ta edición Editorial Mc Graw Hill.
Si deseas leer contenido científico de calidad en habla hispana te invito a revisar la etiqueta #STEM-ESPANOL donde podrás encontrar diversidad de temas, Matemática, Ingeniería, Física, Química, Biología, Medicina, Ciencia, Tecnología y mucho más.
Muy buenas tus tutorias!!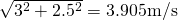 😃
😃
otra forma de interpretar el último resultado de los hombres corriendo sería esta: Si los dos corren en tiempo infinito entonces podemos despreciar el recorrido previo de A, y por tanto la velocidad en que se separan sera la hipotenusa de un triángulo con lados de 3m/s y 2.5m/s, es decir,
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Excelente observación, la velocidad en que separan equivale a la hipotenusa de un triangulo cuyos catetos son las velocidades de ambos corredores, de la forma que se plantea en el artículo se aborda desde la perspectiva de razón de cambio y límites.
Saludos estimado @jga
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
@jga, ¿cómo puedo contactar contigo (Telegram, Reddit, etc.)? Me gustaría hablar contigo de un proyecto relacionado con EOS.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Un saludo @agmontpetit, me puedes escribir por telegram @joticajulian, o discord #jga0699
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muy importante el estudio del cálculo diferencial para todos aquellos fenómenos de la naturaleza que expresan sus comportamientos por medio de razones de cambio.
En mi caso como ingeniero de petróleo son muchos los casos en los que las derivadas aportan a resolver problemas de razón de cambio, entre uno de esos problemas está el planteamiento de la ecuación de darcy para la permeabilidad, el petróleo como fluido se desplaza en el yacimiento por medio del espacio poroso de la roca, esta cantidad de fluido desplazado depende de otros factores como la longitud de la arena, de la porosidad de la roca entre otros más. Todas estas variables son medidas, en las cuales el valor de permeabilidad de la roca se calcula por la ecuación de darcy que es el resultado de la aplicación de razones de cambio.
Saludos amigo @ydavgonzalez, gracias por compartir este contenido.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Interesante la aplicación de la ecuación de Darcy para la permeabilidad, saludos @carlos84.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos @ydavgonzalez, encantada de leer y disfrutar de nuevo leer tus publicaciones: Éxitos para ti este 2019!!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muchas gracias por el apoyo @elvigia. Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola @ydavgonzalez, muy interesante tu aporte, desde la perspectiva educativa tiene las siguientes bondades que la hacen valiosa:
Particularmente creo que a pesar de que existan muchos programas que realicen estos procesos, el estudiante y las nuevas generaciones deben conocer el procedimiento manual, sobre todo el que va a formar a otros en Matemática, por cuanto es vital explicar el proceso formal del cual derivan los resultados, es algo así como cuando se comenzó a utilizar calculadoras científicas, ciertamente son un gran aliado en los temas de Cálculo Matemático, pero el hecho de resolverlo todo con una calculadora hacía que hasta las operaciones más elementales también se hicieran en el referido dispositivo, situación que resultó preocupante en su momento. Muy bueno tu aporte, saludos cordiales!!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Así es @reinaseq muy acertado tu aporte, los estudiantes deben conocer los procedimientos del análisis matemático.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @ydavgonzalez! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board
If you no longer want to receive notifications, reply to this comment with the word
STOPDownvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit