Hola estimados amigos de #stem-espanol y comunidad de steemit en general a continuación les presento un artículo referente a uno de los tópicos más importantes en la Investigación de Operaciones, el cual es el Método Simplex utilizado para resolver Modelos de Programación Lineal.
Pero ustedes se preguntarán ¿Que es un modelo de Programación Lineal?, un Modelo es una representación matemática de la realidad, en cuanto a la programación lineal según Taha(2012)
La programación lineal está diseñada para modelos con funciones objetivo y restricciones lineales

George Dantzig Fuente
Es decir, para poder aplicar la programación lineal el modelo matemático debe constar únicamente de igualdades y desigualdades lineales. En el presente artículo se explicará el Método Simplex que es el más utilizado para resolver modelos de Programacíon Lineal aplicándolo a un problema típico, este método fue creado en 1947 por el matemático norteamericano George Dantzig.
Problema sobre la Elaboración de las Hallacas
La señora Medina elabora hallacas durante todo el año en la ciudad de Coro, en diciembre del año 2017 ella dispone de Bs 5.000.000 para invertirlos en la elaboración de hallacas, el costo para elaborar el relleno de cada hallaca es el siguiente:
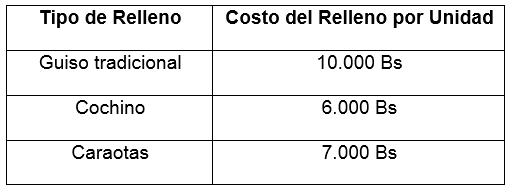
Tabla sobre el costo del relleno. Fuente: Elaboración propia
El costo de las hojas de plátano para envolverlas es de 1.000 Bs por cada hallaca, el costo de la harina y los otros ingredientes es de 8.000 Bs por hallaca, el costo del pabilo gastado para amarrar una hallaca es de 500 bs. La comunidad del sector le solicita a la señora Medina que elabore como máximo 120 hallacas que no sean de guiso tradicional, adicionalmente como medida para controlar el colesterol de la población, la comunidad le ha pedido a la señora Medina que el número de hallacas de guiso tradicional más el doble de hallacas de cochino sea a lo sumo 200, si cada hallaca se vende en 25.000 Bs. Determine los niveles de producción de hallacas que maximizan las ganancias de la señora Medina de conformidad con su presupuesto y las restricciones impuestas por la comunidad.
Formulación del Modelo de Programación Lineal
Analizando el problema se elabora la siguiente tabla que refleja el costo para elaborar cada hallaca (se calcula mediante sumar el costo del relleno, las hojas de plátano, el pabilo, la harina y los otros ingredientes) y la ganancia obtenida
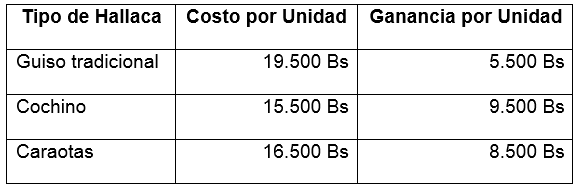
Tabla sobre costos y ganancias. Fuente: Elaboración propia
Las variables de decisión serían el número de hallacas de cada tipo que se desea producir x1 para guiso tradicional, x2 cochino, y x3 caraotas. Una vez determinadas las variables de decisión se efectúan los siguientes pasos:
1° Encontrar la Función Objetivo
La función objetivo representa la medida de efectividad del sistema, es decir, lo que se quiere maximizar o minimizar. Como se quiere maximizar la ganancia la función objetivo queda definida de la siguiente forma
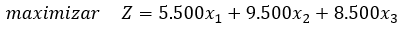
2° Determinar las Restricciones del Modelo
Las restricciones del sistema expresan cantidades de recursos limitados o requerimientos que se deben satisfacer. En relación al presupuesto se dispone de un máximo de Bs 5.000.000 que deben ser invertidos entre todas las hallacas
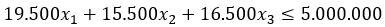
Como la comunidad ha solicitado que como máximo solo 120 hallacas sean de algo diferente al guiso tradicional, es decir, la suma del número de hallacas de cochino y caraotas debe ser como máximo 120, se establece la siguiente restricción
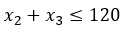
La medida para controlar el colesterol de la población en la comunidad implica que el número de hallacas de guiso tradicional más el doble de hallacas de cochino sea a lo sumo 200, es decir
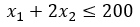
Estableciendo el siguiente modelo de programación lineal
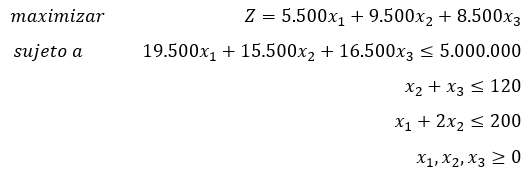
Observe que se incluye al final una restricción de no negatividad debido a que los valores de las variables de decisión no pueden ser negativos ya que representan las cantidades de hallacas de cada tipo elaboradas. Para aplicar el método simplex se expresa el modelo en forma típica en la cual las desigualdades se convierten en igualdades introduciendo variables de holgura de la siguiente forma
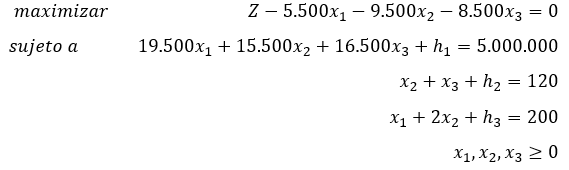
Las variables de holgura deben tomar valores mayores o iguales a cero. Dicho modelo se representa de forma tabular, tal como se muestra a continuación
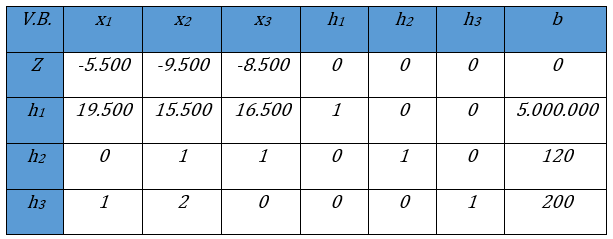
Tabla Inicial del Método Simplex. Fuente: Elaboración propia
Una vez determinada esta forma tabular se procede a resolver aplicando operaciones similares a las transformaciones algebraicas de Gauss-Jordan en matrices, se debe determinar una variable entrante y una variable básica saliente en cada iteración, según Taha (2012) el criterio a usar es el siguiente:
A) La variable de entrada en un problema de maximización (minimización) es la variable no básica con el coeficiente más negativo (positivo) en la fila Z, el óptimo se alcanza en la iteración en las cual los coeficientes en la fila Z son no negativos (no positivos).
B) La variable de salida es la variable básica asociada con la relación mínima no negativa con el denominador estrictamente positivo.
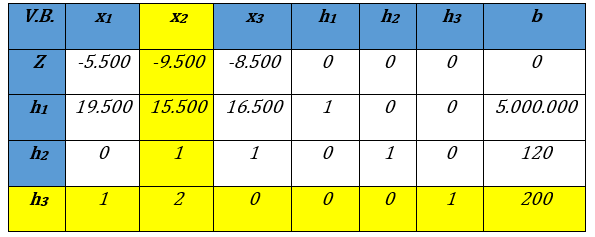
Iteración N° 0 del Método Simplex. Fuente: Elaboración propia
El coeficiente negativo con mayor valor absoluto es -9.500 por lo tanto la VE es x2, calculando las relaciones entre la columna b y la fila seleccionada se obtiene
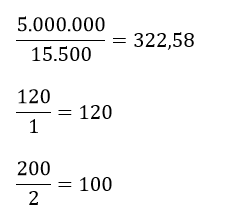
Por lo tanto, la Variable Básica Saliente es h3, luego de esto se aplican operaciones de fila de forma tal que la en la columna seleccionada (columna pivote) todos los elementos sean igual a 0 a excepción del elemento en la intersección entre la fila y la columna seleccionada (elemento pivote, el cual debe ser igual a 1). Se divide la fila 4 entre 2 y se aplican las operaciones de fila obteniendo la siguiente tabla para la iteración N° 1
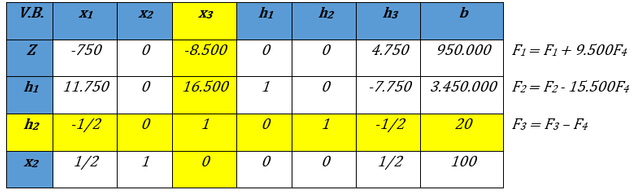
Iteración N° 1 del Método Simplex. Fuente: Elaboración propia
Se procede a iterar nuevamente utilizando los mismos criterios, VE: x3 VBS: h2
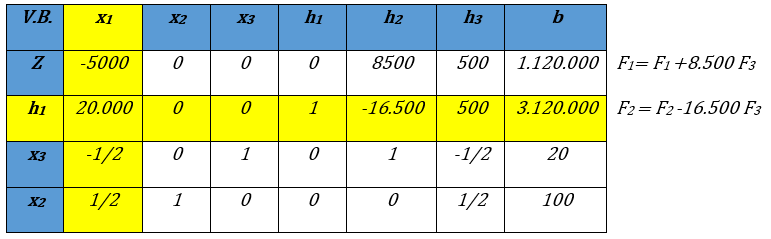
Iteración N° 2 del Método Simplex. Fuente: Elaboración propia
VE: x1 VBS: h1, la fila pivote se divide entre 20.000
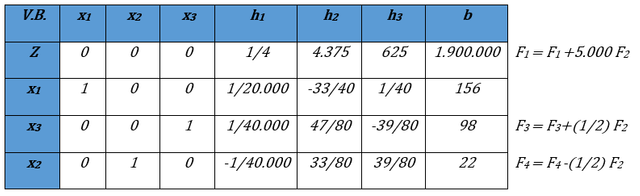
Iteración N° 3 del Método Simplex. Fuente: Elaboración propia
Como todos los valores en la fila Z son positivos, la solución obtenida es óptima, es decir, los valores que maximizan la función objetivo son los siguientes:
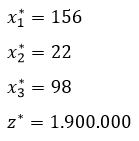
Lo cual para la señora Medina significa que si quiere maximizar sus ganancias debe preparar 156 hallacas de guiso tradicional, 22 de cochino y 98 de caraotas, obteniendo una ganancia total de Bs. 1.900.000, es decir, un 38% de su inversión original. Este tipo de problemas pone en evidencia la utilidad del Método Simplex en contextos de la vida cotidiana permitiendo maximizar las ganancias al realizar una inversión.
Referencias Bibliográficas
Taha, Hamdy A. (2012) Investigación de Operaciones 9° Edición. Editorial Pearson.


Hola @ydavgonzalez, como siempre muy ilustrativo tu desarrollo. Este método tiene algo que ver con los multiplicadores de Lagrange? ya que se asemeja mucho al buscar la optimización en base a restricciones.
Un saludo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos, el método de los multiplicadores de Lagrange es un método de optimización también. sin embargo, se suele usar cuando solo se tienen restricciones de igualdad aunque su alcance abarca problemas con funciones que pueden ser no lineales, mientras que el Método Simplex se enfoca en un tipo de problema muy específico Modelos de Programación Lineal en los cuales tanto la función a optimizar como las restricciones son funciones lineales (sin embargo, las restricciones pueden incluir desigualdades).
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muy buen post @ydavgonzalez, ¿existe algún software que permita realizar estos cálculos? Tú dejas muy claro las bases conceptuales de este método. Imagino que para más variables se requiere el uso de programas. Saludos y felicitaciones por tu post!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias por el apoyo, existen varias alternativas tales como el Lingo o el WinQSB en un próximo artículo estaré abordando el uso de software en la resolución de modelos de programación lineal.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Excelente articulo estimado! Me gusta observar artículos que ademas de ser sumamente informativos aportan una buena manera de resolver problemas de vida cotidiana, en la ciencia esta la respuesta! Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias por el apoyo, Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Si la aplicabillidad en la vida cotidiana es muy importante. Felicidades
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Así es, estimada @isgledysduarte
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muy importante conocer estos métodos para las personas que quieren invertir, sobre todo para nosotros los venezolanos que debido a la situación actual del país no nos podemos dar el lujo de quedar en pérdidas. Excelente @ydavgonzalez!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias por el apoyo, Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Me encanta el ejemplo que utilizas por como llevas a la cotidianidad el empleo de estas herramientas matemática, además lo explicas con una facilidad asombrosa. Excelente aporte!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Estimado @joseleogon, gracias por el apoyo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muy buen artículo @ydavgonzalez.
¡Felicitaciones!.
Excelente aporte. Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos profesor Terenzio Soldovieri @tsoldovieri
¡Que de tiempo!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos @maria1989. Es cierto,
¡Qué de tiempo! jajajajaja 😄
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias por el apoyo @tsoldovieri Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
También me gustó su artículo; y lo más agradable fue que trabajó con las hallacas a muy bajo precio. ¡Que bien!
Saludos Sr. @ydavgonzalez
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias, así es esperemos que en este 2018 aún podamos comerlas a buen precio.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Es muy didactico la verdad . Siempre es bueno encontrar la mejor forma de explotar una ventaja , en este caso optimizar un resultado.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Así es, estimado @vjap55 Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
muy bien aplicado! me gustan los artículos llevados a la vida real, demuestran que si funcionan y son un ejemplo validación científica.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias, dentro de la etiqueta #stem-espanol encontrarás muchos Posts de este tipo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit