Seguridad del Bitcoin ante colisiones hash - Análisis Matemático (Desentrañando los secretos de Bitcoin)

En el artículo anterior analizamos el proceso de generación de la clave pública a partir de la clave privada utilizando la criptografía de curva elíptica (ECDSA), sin embargo, para obtener la dirección bitcoin aún faltan algunos procesos por aplicar conocidos como funciones hash o algoritmos de hashing los cuales toman una entrada que puede ser una cadena de caracteres, una secuencia de bytes o un documento y la procesan aplicando operaciones que no pueden ser revertidas generando una salida única de longitud fija.

Imagen N° 1 HASH160 --- Fuente: Elaboración propia

En el presente artículo analizaremos la seguridad de los algoritmos de hashing utilizados por bitcoin específicamente el SHA-256 y el RIPEMD-160, en primer lugar abordaremos el proceso de obtención de la dirección bitcoin utilizando los algoritmos mencionados.

Ejemplo:

Supongamos que tenemos el número 1 en hexadecimal el cual será la clave privada

00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000001

Al aplicar la multiplicación de curva elíptica obtenemos el punto

X=55066263022277343669578718895168534326250603453777594175500187360389116729240
Y=32670510020758816978083085130507043184471273380659243275938904335757337482424

El cual corresponde a la siguiente clave pública comprimida

0279be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798

Una vez que obtenemos la clave pública comprimida seguimos los siguientes pasos para encontrar la dirección bitcoin:

Paso 1-Se aplica el algoritmo de hashing SHA-256 a la clave pública obteniéndose una secuencia de 256 bits.

0f715baf5d4c2ed329785cef29e562f73488c8a2bb9dbc5700b361d54b9b0554

Paso 2-A la salida obtenida se aplica el algoritmo RIPEMD-160 obteniéndose una secuencia de 160 bits.

751e76e8199196d454941c45d1b3a323f1433bd6

Paso 3- A la salida de los dos algoritmos de hashing se le agrega el byte de versión usado para la red principal de bitcoin 0x00, el resultado será la dirección bitcoin en formato hexadecimal.

00751e76e8199196d454941c45d1b3a323f1433bd6

Paso 4-Para calcular el checksum (mecanismo de verificación para asegurarse que la dirección bitcoin está bien escrita) se aplica el algoritmo SHA-256 dos veces al resultado obtenido en el paso 3, se seleccionan los primeros 4 bytes del último hash SHA-256 los cuales representan el checksum de la dirección bitcoin.

Checksum = 4352f398

Paso 5-Se concatena la dirección obtenida en el paso 3 con el checksum obtenido en el paso 4.

00751e76e8199196d454941c45d1b3a323f1433bd64352f398

Paso 6-Se convierte el resultado obtenido utilizando la codificación Base58Check agregando un 1 a la dirección bitcoin.

1BgGZ9tcN4rm9KBzDn7KprQz87SZ26SAMH

---

Entre tantos algoritmos aplicados surge la pregunta ¿Es posible que dos claves privadas generen la misma dirección bitcoin?

Para responder a esta interrogante primero se debe tener en cuenta el número posible de claves privadas que generan claves públicas diferentes, este número representa el orden de la curva elíptica de Bitcoin secp256k1.

115792089237316195423570985008687907852837564279074904382605163141518161494337

Esto quiere decir que a partir de este número las claves públicas comienzan a repetirse, iniciando un nuevo ciclo, por ejemplo los siguientes números enteros generan la misma dirección bitcoin.

Número entero = 1
Hexadecimal =00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000001
Dirección Bitcoin= 1BgGZ9tcN4rm9KBzDn7KprQz87SZ26SAMH

Número entero=
115792089237316195423570985008687907852837564279074904382605163141518161494338
Hexadecimal= ffffffff ffffffff ffffffff fffffffe baaedce6 af48a03b bfd25e8c d0364142
Dirección Bitcoin= 1BgGZ9tcN4rm9KBzDn7KprQz87SZ26SAMH

¿Sorprendido?, estas dos claves privadas se asocian a una misma dirección debido a que generan la misma clave pública, esto sucede porque al llegar al último punto de la curva elíptica (punto al infinito) se comienza un nuevo ciclo iniciando por el primer punto, sin embargo, en este artículo se aborda un problema diferente, el problema de encontrar dos claves públicas distintas que generen una misma dirección bitcoin.

Se debe recordar que el número posible de claves públicas comprimidas u orden de la curva elíptica es el siguiente:

115792089237316195423570985008687907852837564279074904382605163141518161494337

Este valor es aproximadamente igual a 2²⁵⁶, por lo tanto tenemos un aproximado de 2²⁵⁶ pares clave privada/clave pública, aplicando el primer hash SHA-256 obtendríamos una secuencia de 256 bits, es decir, un total de 2²⁵⁶ valores posibles, por lo tanto la función que aplica el SHA-256 a la clave pública posee el siguiente esquema de entrada-salida:

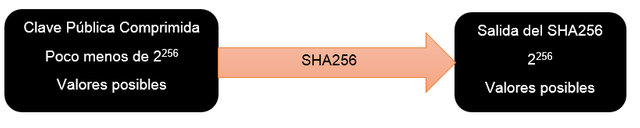
Imagen N° 2 Esquema E-S del algoritmo SHA-256 --- Fuente: Elaboración propia

Se puede apreciar que el número de entradas es menor que el número de salidas esto significa que es posible que cada salida del hash SHA-256 tenga solamente una Clave Pública Comprimida como entrada, sin embargo, este escenario parece improbable debido a la forma en que trabaja el algoritmo SHA-256 el cual opera usando desplazamientos de bits y operaciones que no pueden ser revertidas.

En relación al segundo algoritmo de hashing que se aplica el RIPEMD-160 su esquema de entrada-salida es el siguiente:

Imagen N° 3 Esquema E-S del algoritmo RIPEMD-160 --- Fuente: Elaboración propia

En este caso la salida del hash anterior se toma como entrada del nuevo hash, el número de entradas posibles es mayor que el número de salidas posibles del hash RIPEMD-160:

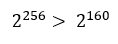
Unificando los dos hash como si se tratara de una función única que suele denominarse HASH160 obtendríamos el siguiente esquema de entrada-salida:

Imagen N° 4 Esquema E-S del algoritmo Hash160 --- Fuente: Elaboración propia

La salida del HASH160 es la dirección bitcoin en formato hexadecimal antes de agregarle el checksum, se puede observar que en la función HASH160 el número de entradas es mucho mayor al número de salidas posibles, esto pone en evidencia la existencia de múltiples entradas que generan la misma salida, es decir, existen claves públicas comprimidas distintas (y por ende claves privadas) que generan exactamente la misma dirección bitcoin.

¿Significa esto que alguien puede gastar los fondos de mi dirección bitcoin con otro par clave privada/clave pública que genere la misma dirección?, en teoría si pero en la práctica encontrar esa otra clave privada es computacionalmente imposible, esto es algo que se conoce como “Colisión Hash” cuando dos entradas producen una misma salida al aplicar un algoritmo de hashing.

¿Cuantas colisiones hash son posibles con la direcciones bitcoin?, debemos recordar la relación entre el número de claves públicas posibles y el número de direcciones posibles. Existen aproximadamente 2²⁵⁶ claves públicas comprimidas posibles y 2¹⁶⁰ direcciones bitcoin posibles, esto significa que como promedio por cada dirección bitcoin se tendrían un número de claves públicas asociadas igual a:

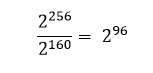
El cual es un número bastante grande equivalente a:

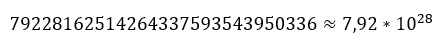
Estamos hablando de 7923 cuatrillones de claves públicas que generan una sola dirección bitcoin como promedio, visto desde esta perspectiva parece fácil encontrar una colisión hash, pero haciendo un análisis más preciso veremos que la probabilidad de encontrarla es insignificante.

Empezaremos calculando la probabilidad de no encontrar una colisión al probar n claves públicas, la probabilidad inversa es la probabilidad buscada, asumimos el número de posibles salidas del algoritmo Hash160 igual a

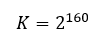
Suponiendo que el algoritmo RIPEMD-160 distribuye las salidas de forma uniforme, la probabilidad de no encontrar una colisión en el primer intento es

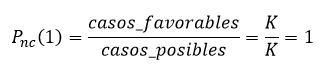
Evidentemente es imposible encontrar una colisión en el primer intento pues solo tenemos una dirección, para él segundo intento, la probabilidad no haber encontrado una colisión es

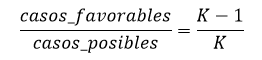
Debido a que hay K-1 valores diferentes al valor encontrado anteriormente, combinando ambos valores la probabilidad de no encontrar una colisión en los primeros dos intentos es

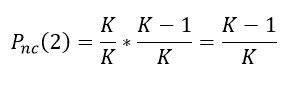
Para los primeros tres intentos

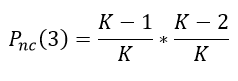
Luego para n intentos

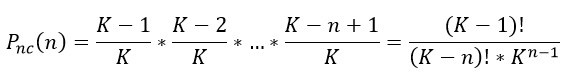
Esta fórmula es difícil de usar en la práctica debido a que el elevado valor de K genera factoriales extremadamente grandes, y de usar la primera fórmula se requerirían muchos cálculos para valores grandes de n. Sin embargo, podemos establecer una cota mínima a P_nc(n) teniendo en cuenta que cualquiera de los términos del producto es mayor o igual que el último término:

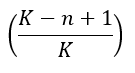
Debido a que en la formula aparecen n-1 términos se cumple

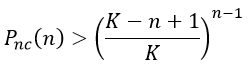
Al calcular la probabilidad inversa obtenemos la probabilidad de obtener una colisión hash en una dirección bitcoin al calcular el hash de n claves públicas P_c(n) la cual es siempre menor a la siguiente cota:

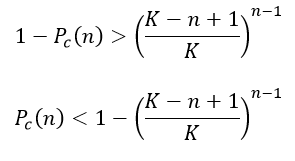
Supongamos que realizamos 10²⁴ intentos de encontrar una colisión

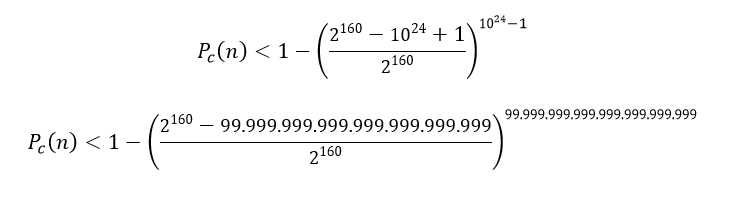
Utilizando la calculadora de wolframalpha.com

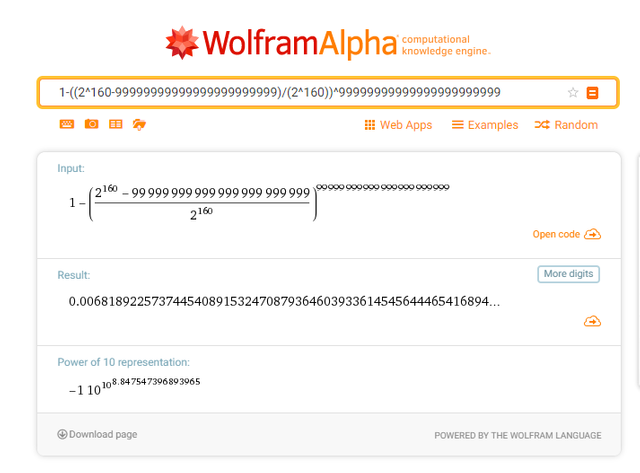
Imagen N° 5 Uso de wolframalpha.com para calcular P_c(n) --- Fuente: Elaboración propia

Finalmente obtenemos

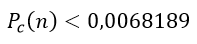
Esto quiere decir que realizando un cuatrillón de intentos tendríamos una probabilidad menor al 0,681892% de encontrar una colisión hash, para hacernos una idea de la magnitud este número si tuviéramos un millón de computadoras encontrando un millón de direcciones bitcoin por segundo tardaríamos más de 30.000 años para encontrar una colisión hash. También debemos recordar que el valor que hemos calculado es una cota máxima, el valor real está muy por debajo de esa cantidad debido a que la mayoría de los términos del producto son mayores al valor asumido en la aproximación.

En base a este análisis podemos apreciar la dificultad de encontrar una colisión hash, por este motivo los algoritmos hash SHA-256 y RIPEMD-160 se consideran resistentes a colisiones, así que por ahora nuestros bitcoin están seguros y en caso de que se detectara alguna vulnerabilidad en cualquiera de los algoritmos de hashing de bitcoin se podría modificar el protocolo de bitcoin haciéndolo seguro nuevamente.