Al-Kuhi는 페르시아의 수학자, 물리학 자, 천문학 자였으며, 수학과 천문학에 관한 많은 저술을 통해 가장 위대한 이슬람 기하학 학자 중 한 명으로 여겨집니다.
Al-Kuhi는 940 년이란의 Tabaristan에있는 Kuhi라는 마을에서 태어났습니다. 이 마을의 이름에 따르면 그는 역사상 알쿠 히로 알려져 있으며 그의 정식 이름은 아부 사할 와이 잔 이븐 루스 탐 알 쿠히입니다.
그의 이름과 함께 'Rustam'이라는 단어는 그가 유명한 페르시아 영웅 Rustam의 후손임을 나타냅니다. 그는 수학자이자 천문학 자였습니다. 그의 연구의 주요 분야는 기하학이었습니다.
현대 과학자들은 그를 최고의 수학자로 간주했으며 Omar Khayyam은 그를 최고의 수학자로 간주했습니다. Kuhi는 그의 글에서 기하학적 문제를 해결합니다. 그 후 그의 기하학적 솔루션이 방향으로 사용됩니다.
그는 Bouedian 왕조가 설립되었을 때이란에서 자랐습니다. Bouadian 왕조는 945 년부터 1055 년까지 서부이란과 이라크를 통치했습니다. 945 년 아흐메드 바이 (Ahmed Buye)는 압바스 왕조의 수도 인 바그다드를 점령했습니다. 949 년부터 943 년까지 Adud Ad-Daula 통치 기간 동안 Bouadian 왕조의 통치는 번영의 절정에 도달했습니다. 바그다드에서 그는이란 남부와 현재의 이라크 대부분을 통치했습니다. 과학과 예술의 위대한 후원자 인 Adud al-Dawla는 al-Kuhi, Abul Wafa 및 al-Sijji를 포함하여 바그다드의 왕실에 많은 수학자를 수용했습니다.
989 년 Adud Ad-Daulah는 시라즈의 암과 염소 자리 관찰을 명령했습니다. 989/980 년에 Al-Kuhi, Al-Sijji 및 기타 천문학 자들은 Siraj에서 Tropic of Cancer와 Capricorn을 관찰했습니다.
Adud ad-Daulah의 아들 Sharaf ud-Daulah는 963 년 칼리프로 임명되었습니다. 그가 수학자와 천문학 자들을 계속 지원하면서 알-쿠히는 바그다드에서 새로운 칼리프를 위해 일할 기회를 가졌습니다. Caliph Sharaf ud-Daulah는 천문학 자 al-Kuhi에게 여섯 개의 행성을 관찰하도록 지시했습니다. 바그다드 왕궁에 알쿠 히르 전망대가 세워졌습니다.
우물 설계에 따라 전망대에 필요한 장비를 제작하여 건물 공사가 완료되면 그곳에 배치됩니다. Al-Kuhi는 천문 대장으로 임명되었고, 천문대는 96 년 6 월에 공식적으로 개장했습니다. 개막식에는 많은 천문학 자들이 참석했습니다. Abul Wafa는 현재 천문학 자 중 한 명이었습니다. 그는 또한 Sharaf ud-Daulah의 왕실에 임명되었습니다. 전망대 개막식에 참석 한 또 다른 사람은 Abu Ishaq al-Sabi였습니다. Al-Sabi는 바그다드 법원의 고위 관리였습니다. 그는 수학에 관심이있었습니다.
96 년에 Kuhi는 바그다드에있는 Sharaf ud-Daulah 궁전 정원에서 행성과 별을 관찰했습니다. 관측하는 동안 많은 천문학 자들이 있었다. Sharaf ud-Daulah가 989 년에 사망했을 때 바그다드 천문대는 운영을 중단했습니다. 이때 보이드 제국은 붕괴 직전이었다. 경제 불황은 군부의 쿠데타로 이어져 통치자의 삶을 비참하게 만들었습니다. 행성과 별을 관찰하는 것은 조수가 필요합니다.
Al-Kuhi는 기하학적 드로잉에 사용되는 나침반의 발명가입니다. 그는 Risala Phil Barker Al-Tam (완벽한 나침반에서)의 첫 번째 입자 나침반을 설명했습니다.
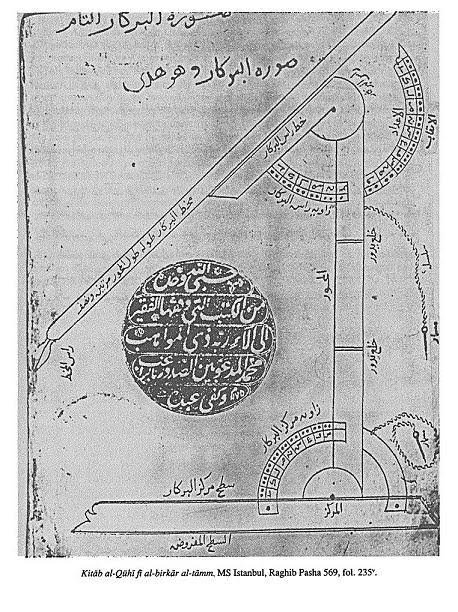
Kuhi는 처음에는이 한쪽 다리가있는 나침반을 사용하여 직선, 원, 타원 및 각도를 그렸습니다. 책에서 그는 다양한 악기를 만드는 기술을 설명했습니다. 그는 누구나 쉽게 천체 실험실, 해시계 및 유사한 장치를 만들 수 있다고 생각했습니다.
Al-Kuhi는 또한 그의 논문 Phil Barker Al-Tam의 일부에서 천체 실험실 구축 문제에 대해 논의합니다. 그의 책은 두 부분으로 나뉩니다. 첫 번째 부분에는 4 개의 장이 있고 두 번째 부분에는 7 개의 장이 있습니다. Al-Kuhi는 그의 책에서지도를 그리는 문제를 해결했습니다.
Al-Kuhi는 그리스인의 우월한 기하학을 이슬람 세계에 부활시키고 도입하는 데 주도적 인 역할을했습니다. 그는 기하학에서 2 차 방정식과 조밀 방정식을 풀었습니다.
즉, 모서리에있는 특정 원의 크기와 동일한 원을 그리고 다른 원의 볼륨과 동일한 두 번째 원을 그리는 문제는 동일합니다. 그러나 아르키메데스가 제시 한 문제에 대한 해결책은 해결책보다 더 어려웠습니다. Al-Kuhi는 과장법을 사용하여 직각 타원을 이등분하여 두 개의 알려지지 않은 길이를 그리고 그가 문제를 해결 한 조건에 대해 논의합니다.
Euclid의 Elements, Appelnius의 Conix 및 Archimedes의 On the Sphere and Cylinder의 결과를 사용하여이 기하학적 문제를 해결하는 고전적인 방법이었습니다. Al-Kuhi는 구석에 솔루션이 존재한다면 좌표가 있어야한다는 것을 증명했습니다. 좌표의 위치는 모서리에 그려진 직사각형 타원 내에 있습니다.
확실히 al-Kuhi는 현대의 문자 적 의미에서 그의 수학적 아이디어를 표현하지 않았습니다. 오히려 그는 고대 그리스 수학의 전통적인 고전 기하학에서 자신의 아이디어를 표현합니다. Kuhi는 표면의 각도를 소개합니다. 해법이 쌍곡선의 좌표에 있음을 보여줍니다. 그런 다음 두 곡선을 이등분하여 문제가 잘 해결됩니다.
그는 설명적인 기하학적 방법과 유사한 방법을 사용하여 게일에 원을 그렸습니다. Kuhi는 그의 'Risala fi Kismat al-Jabiya'(각각의 삼분면)에서 과장법의 도움으로 각도를 삼각형으로 만드는 이슬람 솔루션을 제공합니다. 수학자 al-Sijji는 그의 방법을 따랐다.
Kuhir의 'Risala fi Istikharaj dil al-Musabba al-Mutasabil-Adla'(정규 칠각형 건설에 관한)에서 각도의 삼각 분할을 그리는 방법은 아르키메데스보다 더 수용 가능했습니다. 그는 1 : 2 : 3 비율의 각도로 삼각형을 그립니다. Kuhi는 쌍곡선과 타원을 이등분하고 동일한 매개 변수에 언급 된 비율의 팔을 그립니다.
Al-Sijji는 그의 방법을 정확히 따랐습니다. "Risala fi amal mukhamas Musabil al-Adla fi Murabba Malum '(알려진 정사각형에 정방형 오각형 구성) -4 019-PR은 두 각도를 이등분하여 주어진 정사각형에 직각 오각형을 그리는 문제를 해결합니다. 이번에는 두 가지 하이브리드의 도움을 받았습니다. Kuhi는 Euclid의 Elements 1 ~ 5 장, Euclid의 데이터, Appelnius의 Conix 1 ~ 3 장의 일부를 통해 오각형을 그리는 솔루션을 알아 냈습니다. 이 Kuhir의 그림은 과장의 원래 디렉토리의 종교를 증명하기 때문에 중요합니다.
그는 독립적으로 상피 디렉토리의 종교를 발명하고 증명했으며 Appelnius보다 한 걸음 더 나아갔습니다. Risala fi Istiqraj Misahat al-Mujassam al-Muqafi에서 Kuhi는 아르키메데스보다 더 간단하고 명확한 솔루션을 제공합니다.
정사각형에 오각형을 그리는 것은 불가능하지만 오른쪽 오각형을 그리는 방법에는 두 가지가 있습니다. 첫 번째 방법은 "2 차 방정식"입니다. 9 세기에 Abu Kamil은이 문제를 해결했습니다. 두 번째 방법은 '밀집 방정식'입니다. Al-Kuhi는 두 번째 접근 방식을 취했습니다. Kuhir의 Risala Fi Istiqraj Misahat Al-Mujassam Al-Muqafi는 1947 년 인도 하이데라바드에있는 Osmania Oriental Publishing에서 출판되었습니다.
al-Kuhi와 수학에 관심이있는 고위 공무원 Abu Ishaq al-Sabir 사이에는 긴밀한 접촉이있었습니다. Al-Kuhi와 Al-Sabir 사이에 편지가 교환되었습니다. 8 개의 편지가 서로 교환되었지만 4 개의 세부 사항이 발견되었습니다. 그들은 수학 문제에 대한 편지를 교환했습니다. Kuhi는 편지에서 '원과 나와 m이 서로 교차하는 직선이 주어진다고 가정 해보자. 원의 모서리에있는 점을 상기하십시오. 이 지점에서 접선은 L과 결합하고 m은 M과 결합합니다. 그렇다면 TL을 선택하는 방법 : TM은 특정 비율이 될 것입니다. 잎 중 하나는 매우 흥미 롭습니다. 이 편지에서 Kuhi는 다양한 인물의 초점과 관련된 7 가지 공리를 설명합니다. 6 개 중 5 개 결과가 정확합니다. 그러나 여섯 번째는 틀 렸습니다. 즉, 반원의 중심은 3 : 7의 비율로 반경을 나눕니다. 이 잘못된 결과로부터 Al-Kuhi는 i = 28이라는 동일한 오류를 결론지었습니다. 이것은 최고의 수학자조차도 실수를 할 수 있음을 증명합니다.
Al-Kuhi는 수학과 천문학에 관한 많은 책을 썼습니다. 기하학에 대한 그의 열정은 높았습니다. 그는 기하학에 관한 약 30 권의 책을 저술했습니다.
그는 아르키메데스와 아펠 레니 우스의 기하학적 문제에 집중했습니다. 이 연구에서 3 차원 및 4 차원 방정식을 푸는 문제가 발생합니다. 그는 많은 문제를 해결하는 데 성공했고 해결책을 찾았습니다. 그들 중 하나는 특정 은하의 어떤 부분과 동일합니다.-부피는 다른 부분을 그리는 방법입니다. Marton에 따르면 al-Kuhir의 기하학은 아랍 기하학 중 가장 위대한 기하학입니다.
그는 1000 년에 죽었습니다.
함께 해주셔서 감사합니다
감사 @upvu,@nutbox.mine,@zzan.witnesses, @steemzzang, @zzan.hmy