Find the Real Root of 4^x + 6^x = 9^x

Given a equation 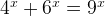$4^x + 6^x = 9^x$ , let’s find the real value of x.

First, divide both sides by 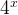$4^x$ which becomes:

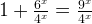
$1 + \frac{6^x}{4^x} = \frac{9^x}{4^x}$
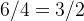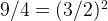as $6/4 = 3/2$ , and $9/4 = (3/2)^2$ , it becomes:

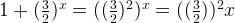
$1 + (\frac{3}{2}) ^x = ((\frac{3}{2})^2)^x = ((\frac{3}{2}))^2x$

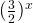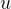Let’s replace $(\frac{3}{2}) ^x$ with $u$ and further we have:

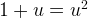$1 + u = u^2$ that is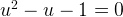 $u^2 - u - 1 = 0$

This equation has a golden root (the negative root should be discarded):

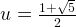
$u = \frac{1 + \sqrt{5}}{2}$

Therefore, 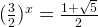$(\frac{3}{2}) ^x = \frac{1 + \sqrt{5}}{2}$
and $x = \log_{\frac{3}{2}}^{\frac{1 + \sqrt{5}}{2}}$
and $x = \frac{\ln{\frac{1 + \sqrt{5}}{2}}}{\ln{\frac{3}{2}}}$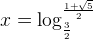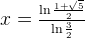
and we can compute the value x that is approximately 1.187.

--EOF (The Ultimate Computing & Technology Blog) --

Reposted to Blog

Every little helps! I hope this helps!

Steem On!~

If you like my work, please consider voting for me or Buy Me a Coffee, thanks!
https://steemit.com/~witnesses type in justyy and click VOTE

Alternatively, you could proxy to me if you are too lazy to vote!