
매장된 이더 물리에 대한 개인적 호기심 탐구 시리즈입니다.
아인슈타인의 상대성 이론, 소립자, 양자역학을 짚어보고, 궁극적으로 이더 물리를 파헤칩니다.
이전글 - [Aether 물리] #25 양자역학편 - 기본 상호작용, 일출
촛불을 자세히 보면 몇 가지 색이 보입니다.

그런가? 할 수 있지만, 여기에 매우 특이한 사실이 숨어 있습니다. 촛불과 같은 발열체에서 우리가 보는 색과 온도는 매우 밀접한 관계가 있습니다.
뜨거운 물체에서 나오는 빛은 오로지 물체의 온도에 따라서만 색이 바뀐다.
그래서 특정 온도에서 나오는 빛의 파장의 강도를 측정하여 그래프로 그릴 수 있습니다.
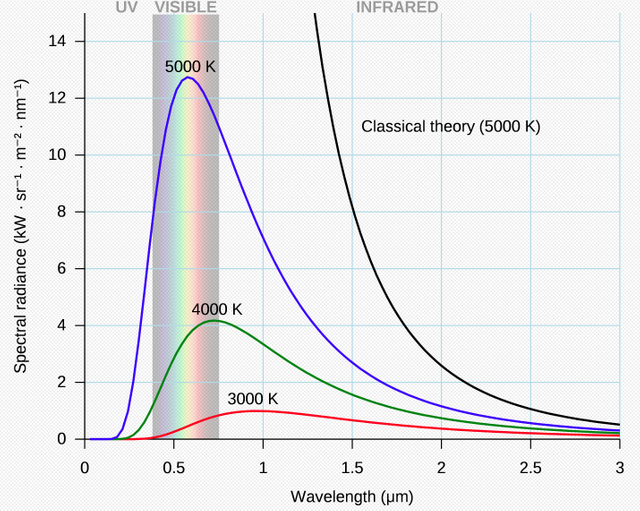
이 그래프만 있으면, 발열체의 온도를 빛의 파장만 보고서도 알 수 있게 됩니다! 이러한 원리로 멀리 떨어져 있는 별들의 온도를 측정할 수 있게 되는 것이죠.
참고로, 파장은 진동수, 즉 주파수와 반비례 관계에 있습니다. 파장이 길면, 주파수가 짧습니다. 적외선은 가시광선보다 파장이 길고, 주파수는 낮습니다. 위 그래프에서 온도 기호인 K는 절대온도 기호입니다. 3000K는 3000-273.15는 대략 섭씨 2,726도가 됩니다.
위 그래프를 보면, 온도마다 최대 강도가 되는 파장이 다릅니다. 3000K의 물체는 파장이 0.9um 부근에서 최대 강도가 나타납니다. 5000K의 물체는 파장이 0.5um 부근에서 최대 강도가 됩니다. 이처럼 온도가 올라갈수록 최대 강도 파장이 작아집니다. 즉 주파수는 높아집니다.
중요한 점은, 이 최대 강도를 되는 위치는 순전히 온도에만 영향을 받는다는 것입니다. 참고로 하얗게 타는 물체는 실제 하얀색의 파장의 빛(하얀색 파장의 빛은 없습니다)이 아니라, 가시광선 영역의 여러 파장의 빛이 섞여서 하양게 보이는 것입니다.
그런데 그래프를 잘 살펴보면, classic theory(고전 이론) 그래프도 나타나 있는데, 파장이 짧아질수록 강도가 무한대로 발산합니다. 고전이론에서 이와 같이 파장이 짧아지면 무한대의 에너지가 방출되는 모순점이 있었습니다. 이것을 자외선 파탄(ultraviolet catastrophe)라고 합니다.
이 문제의 해결이 바로 양자역학의 시작입니다.
양자 가설
막스 플랑크는 이 문제를 고전이론과는 완전히 다른 이론으로 해결하고자 했습니다. 이 때까지만 해도 빛은 파동이라는 이론이 지배적이었습니다. 지금은 빛이 파동과 입자 두가지 성질을 가진다고 인정하지만요 (사실 빛의 이중성도 애매합니다. 빛은 파동처럼 행동하고, 입자처럼 행동하기도 한다고 하니 말입니다.)
플랑크는 물체마다 진동자(oscillator)라는 것이 있다고 가정했습니다. 여기서 각각의 진동자는 한 가치 진동수의 빛만 방출합니다 진동자 자체는 고유의 에너지를 갖는데, 그 값은 진동수에 아주 작은 상수값을 곱한 만큼입니다. 그리고 하나의 진동자가 내보내는 빛의 양은 그 고유 에너지의 정수로 된 배수만 가능하다고 가정했습니다.
간단히 말하면, 물체마다 특정 진동수를 가진 진동자들이 있고, 이 진동자들이 내보내는 에너지가 연속이 아니라 불연속적인 값이라는 것입니다. 플랑크는 이 불연속 에너지를 라틴어로 "얼마나"라는 뜻의 퀀텀(quantum)이라고 지었습니다. 우리가 개수를 셀 때 얼마나 있나하는 것처럼, 에너지를 하나 하나 카운트 한다고 가정한 것입니다.
플랑크가 양자역학의 시작을 연 사람이긴 하지만, 그는 고전 물리를 다루는 사람이었습니다. 현상을 설명하기 위해 꼼수처럼 에너지를 양자화한 것입니다. 일단 에너지를 양자화해서 수식을 만들고, 아래 구분구적분 방법처럼, 변수를 무한대로 작게하여 연속적인 에너지가 얻어질 것이라고 기대했습니다.
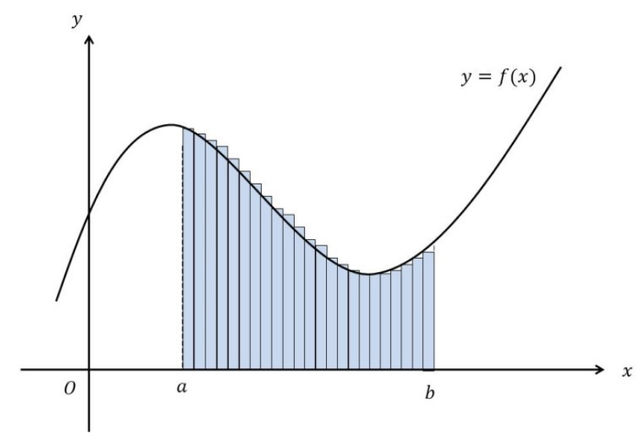
그러나, 아무리 해도 에너지는 불연속적이었습니다. 그가 사용한 매우 작은 상수값은 바로 오늘날 플랑크 상수라 불리는 것으로, 물리적으로 의미를 갖는 최소 길이와 최소 시간 단위로도 쓰입니다.
플랑크 길이: 10^-35m
플랑크 시간: 광자가 빛의 속도로 플랑크 길이를 이동하는데 걸리는 시간 -> 10^-44초
플랑크 본인이 가장 당황해했습니다. 말도 안되는 가설을 세우고 연구를 했는데, 그 말도 안되는 가설이 맞는 것입니다! 양자역학의 역사는 그야말로 비논리의 시대입니다. 논리적으로 생각하면 양자역학은 맞지 않게 되는 것이죠.
우리가 많이 들어본 양자도약(quantum jump)라는 말도, 보어의 말도 안되는 주장이었습니다. 파울리의 배타원리에 따르면 전자는 특정 층(레이어)에만 존재할 수 있습니다. 전자가 한 레이어에서 다른 레이어로 이동하는 현상이 발생하는데, 이동하려면 그 레이어 사이를 움직이는 것이 상식적입니다. 그러나 이것은 배타원리에 위배되는 것이죠. 그래서 보어는 이렇게 얘기합니다.
전자는 한 레이어에서 사라져서 다른 레이어에 순간 이동한다!
양자역학은 이러한 비상식적 가설이 넘쳐납니다. 우리의 상식으로 이해할 수 없는 분야이죠. 현재 주류 물리학도 근본원리보다는 현상을 설명하는데 초점을 맞추는거 같습니다.
플랑크 발견의 실생활 응용
그럼 플랑크의 발견이 우리 생활에 어떤 영향을 끼쳤을까요? 사실 우리에게 중요한 것은 플랑크 상수의 의미도 아니고, 터무니없는 이론도 아닙니다. 우리가 직접적으로 느끼는 무언가를 원하죠.
앞서 잠깐 말했듯이 플랑크의 발견으로 태양 표면의 온도나 멀리 떨어진 별들의 온도를 측정할 수가 있게 됩니다. 더욱 실생활에 밀접한 예는 적외선 체온 측정계입니다. 플랑크 공식을 이용해서 물체에서 나오는 적외선 총량을 측정하면, 물체의 온도를 알 수 있게 되는 것입니다.

이 밖에도 빛과 온도의 관계를 이용하면 많은 응용이 있겠죠.