퀴즈 131 초승달 쪼개기
초승달 (원의 넓이로 보았을 때 1/4 만 남아 있다고 하자)을 5개의 직선으로 쪼갠다고 할 때 최대 몇 조각이 만들어지겠는가
21개.. 그림 안습 그림판 그리기 실패..
퀴즈 132 고속도로의 길이
Steemit 시와 EOS 를 있는 고속도로 하나를 생각하자. 차 한대는 Steemit 시로부터 EOS 로 다른 차 한대는 EOS에서 Steemit 으로 출발한다고 하자. 그리고 어떤 차인지는 모르지만 두 차의 속도는 다르다고 하자.
이 두 차는 먼저 가까운 도시의 72 km 가 되는 지점에서 서로를 스쳐 지나갔다. 서로 각자의 도시에 도착하여 일을 마치고 다시 원래의 도시로 돌아가기로 했다.
이번에는 처음과 반대쪽의 도시에서 40km 떨어진 곳에서 서로 스치게 됬는데, 이 때 이 고속도로의 길이는 몇 km 인가?
이 문제는 아주 유명한 로이드의 퍼즐 문제로 나도 처음 이 문제를 접했을 때 쉽게 풀지 못했다.
일단 그림을 이용한 풀이를 설명해보자.
1 . 그림을 이용한 풀이
일단 편의상 Steemit 을 A EOS 를 B로 하고 B 에서 출발하는 배의 속도가 A 보다 느리다고 하자. 두 사이의 거리는 L 이라 하자.
그러면 처음 만나는 지점은
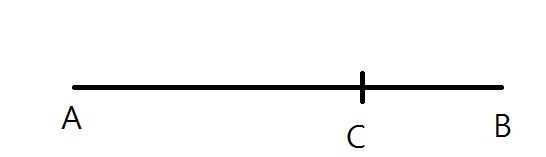
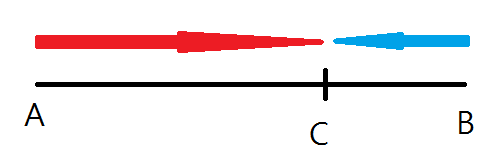
이미 C 점에서 A 와 B 가 총 간 거리는 두 고속도로의 폭 L 이다.
자 이제 양쪽 끝을 찍고 다시 만나는 점 D 를 표시해 보자
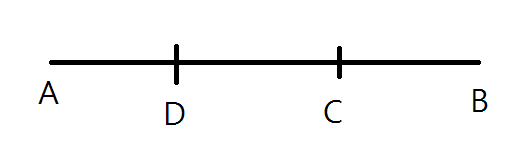
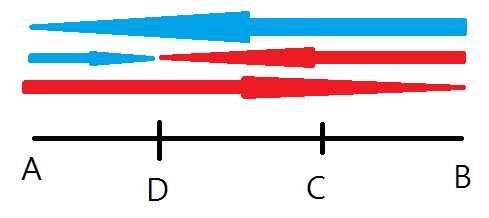
즉 A 와 B 가 각 간 거리의 총 합은 고속도로 폭의 3배
자 여기서 사실 수식으로 풀 수 있는데 조금 더 머리를 써 보자.
처음 C 점에서 만나고 그 뒤 A 와 B 의 움직임에 집중해보자
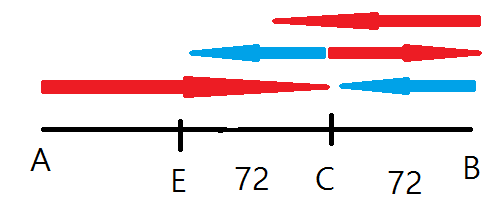
자 D 에서 다시 만났을 때(이 때 A 와 B 가 총 간 거리는 3L 처음 A 와 B 가 만났을 때 두 사람이 간 거리는 L! 이 것으로 부터 B 가 다시만날 때 까지 간 거리는 72x3 인 것을 캐치해야 하는 것이 그림으로 보는 풀이의 핵심이다.) B 가 간 거리는 72x3 인데 40km 떨어진 곳에서 만났으니 실제로 고속도로의 길이는 72x3-40=176 이 된다!
2. 수식을 이용한 풀이
사실 이 문제는 수식으로 접근하면 답이 잘 안나올 수 있다. 왜냐 얼핏하면 2L=2L 이나 L=0 이 나와버리기 때문이다. [실제로 나도 처음에... 댓글을 달아주신 @dj-on-steem 님도 여기에 낚였다..]

자 그림 말고도 수식으로도 똑같이 풀여야 하기에 오랜만에 수식으로 이 문제를 풀어봤다.

변수는 5개고 식은 4개라 모든 값을 풀 수는 없다. 그러나 L 은 정확하게 구할 수 있다가 이 문제의 핵심이다. [에라 알고보니 코텍이 안 깔려 있어서 대강 영어로 적었다... lapsed 인가 lapse 인가 영어를 안 쓴지가 너무 오래되서 에라 몰라 ㅋㅋㅋ 대충 의미는 알아 들었을 것이라 믿는다]
[quiz 133] 시침과 분침
12시 이후 그 다음으로 시침과 분침이 겹치게 되는 시각은? [분수로 표시해보자]
c.f) 12시간 동안 시침과 분침이 몇번 겹치겠는가?
시계 문제는 정말 초 중고 수학 문제의 단골이다.
시침과 분침은 12시간마다 11회 만난다. 12x60/11즉 1번 만날 때마다 걸리는 시간은 65분 27과 3/11 초! 즉 다음에 만나는 시간은 1시 5분 27 과 3/11 초!
이번주 퀴즈 풀이 끝!!!
2는 풀이도 어렵네요. ㅠ.ㅠ
3은.. 제 답이 틀렸군요. ㅋㅋㅋ
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
ㅎㅎ 실수 할 수도 있죠. 어제 시계 문제 좀 많이 풀어봤는데 재밌는 문제들 수집해서 올려보도록 할게요!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
고속도로 문제에서 자동차 2대가 각 도시에서 아무 일도 안보고 찍고 돌아오는 거였나요? 원 문제에선 무언가 일을 본다고 했던 것 같은데.. ^^;; 무언가 일을 보고 또다시 동시 출발로 식을 세웠더니 엉망이 된 거 였네요 ㅎㅎ
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
각 도시에서 보내는 시간이 같다면 그게 얼마나 걸리는지 중요하지 않지요
원문에는 각각 1시간이었나 쉬고 출발하는 거였을 거에요
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
수식은 시간이 같다고 놓으면, 변수 3개에 식 2개면 됩니다.
72/a=(x-72)/b
x/a+40/a=x/b+(x-40)/b [두 차가 각 도시에서 같은 시간 머물렀다면 여기서는 서로 상쇄되네요]
위 아래의 두 차의 속도 a와 b가 공통이므로
72:(x-72)=(x+40):(2x-40)
그래서 x=176.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hi @beoped!
Your post was upvoted by @steem-ua, new Steem dApp, using UserAuthority for algorithmic post curation!
Your UA account score is currently 3.552 which ranks you at #5991 across all Steem accounts.
Your rank has improved 5 places in the last three days (old rank 5996).
In our last Algorithmic Curation Round, consisting of 231 contributions, your post is ranked at #160.
Evaluation of your UA score:
Feel free to join our @steem-ua Discord server
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit