In many statistical data sets, a confidence interval is used as a way of evaluating the observed values of a certain variable. This essentially suggests a range of possible values for an unknown variable. The interval has a corresponding confidence level that the actual value is in the specified range.
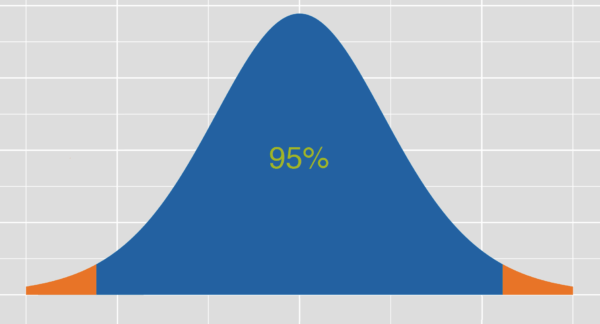
A simple example of statistical confidence intervals is given by studying how the value of a temperature can vary over time. If we use a standard deviation as our standard measure for the value of a parameter of this nature, then a normal curve can be seen as being a better fit to the data than a more exaggerated curve. So if we take one set of data and look at it over a period of time, and the standard deviation tells us that there is a normal range, then we can easily tell that a normal curve is more likely to be more accurate.
Now, a normal curve is very useful to us as it helps us measure a range over a range of data. It is, however, only one measure of a range. It may be best to look at a different parameter instead. This means we can see that the curve is no longer normal and that we have to look at a slightly different parameter to get a better fit.
A confidence interval gives us another option. Rather than look at a parameter as a normal curve, and then looking at the value of this parameter, we look at another parameter first, then we can decide whether we want to accept the current value or not.
There are also cases where the confidence interval fails to give us the right results. One such case is where we get the data as a normal curve with a very high value, and we find that there are many more points in this range that are above the mean. We can be sure that the value of this parameter must be very high in order for this value to be statistically significant.
A high confidence interval gives us another problem. We need to assume that there are many more values outside this range, so that it does not matter that many of these values are near to the mean. However, it is not obvious that there are more than four values outside the range, so that they can all be ignored.
A parameter of this kind can be estimated by using a statistical package called a statistic distribution. This is often done with R but can also be done with the packages of other statistical packages. Using R can give a number of parameters which can be used as well as a mean and standard deviation. This then gives a more complete picture of what is being studied.
When the data has been plotted against the parameter, the results are often called confidence intervals. They are used to help in determining the value of the parameter. They are the simplest way of estimating the probability.
The confidence interval can also give us the chance of getting a certain value of a parameter from the data, but still having the chance of getting a different value. This gives us the "confidence of an estimate". It can also be considered as an estimate of the strength of the relationship between two parameters.
The confidence interval is usually used in conjunction with the mean and standard deviation. These are the two main ways in which the relationship between the parameters is measured.
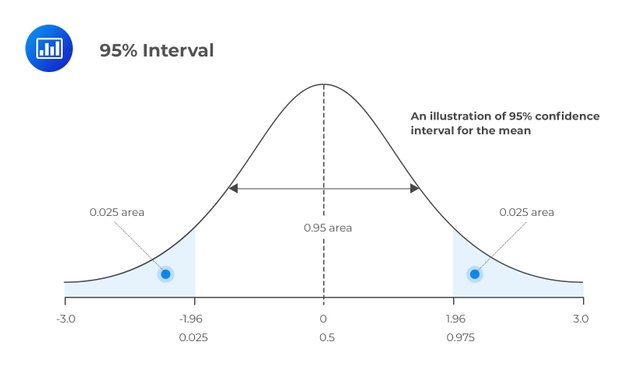
A confidence interval can be calculated by taking two or more measurements and then putting them in the same chart. If they are plotted against the parameter, you will get an idea of the range where the relationship lies. Once you know this, you can get an idea of the probability of getting this relationship given by looking at the data. using the confidence interval as a function of the parameter.
There are times when you can get a better estimate of the parameter using this method. Sometimes, even when there is only one parameter, it is still worthwhile to calculate the interval by using a statistical package.