[수학자 이야기#6] Carl Friedrich Gauss(가우스)

안녕하세요 @yurizard (주노쌤)입니다. 정말 오랫만에 여유가 잠깐 생겨서 수학자 이야기를 작성해보려고 합니다. 제가 생각하는 3대 수학자 중에 드디어 마지막인 가우스에 대해서 소개해볼까 생각합니다.

사실 가우스는 너무나 많은 위대한 업적을 가진 수학자이기에 이야기할 것이 너무나 많은 수학자이지만 오늘은 가우스 기호및 가우스 함수에 대해서 소개하려고 합니다. 굳이 이 내용을 선택한 이유는 요즘 특강으로 고1 수학 수업을 하고 있는데 함수 부분에서 학생들이 은근 가우스 기호 및 가우스 함수의 어려움을 느끼고 있어서 그 부분에 대해서 소개해보고 싶다는 생각이 들었습니다.

Carl Friedrich Gauss(가우스 1777.4.30~1855.2.23 독일)
독일에서 태어난 수학자이지 사실 거의 모든 수학분야에서 위대한 업적을 남겼습니다. 사람들은 그를 19세기 최대의 수학자라고 칭송하고 있으며, 그밖에 물리학에서도 엄청나게 큰 업적을 남깁니다. 상당히 가난한 집에서 태어난 가우스는 어렸을 때부터 신동으로의 자질을 보였으며 가족들 노력으로 공부를 할 수 있었습니다. 만약 가족들이 어려운 형편에 노력해주지 않았다면 우리는 위대한 수학자 한명을 얻지 못했을지도 모릅니다.

이제 소개할 가우스 기호와 가우스 함수에 대해서 알아보고자 합니다.

1. 가우스 기호 [x]
   [x]: x를 넘지 않는 최대 정수

예를 들면 [4.2]는 4.2라는 수를 넘지 않은 최대의 정수이므로 4가 됩니다. 즉 [4.2]=4라고 생각하면 됩니다. 학생들이 가장 많이 실수하는 부분이 바로 음수에서의 가우스 기호입니다. [-4.2]는 -4.2를 넘지 않은 최대 정수입니다. 음수는 숫자가 클수록 더 작은 수 입니다. 그렇기 때문에 [-4.2]= -5가 됩니다. 그러나 많은 학생들이 집중을 하지 않거나 단순하게 생각하고 [-4.2]= -4로 적는 경우가 많이 나옵니다.

※ 가우스의 기호의 성질

1. 가우스 함수 y=[x]
   
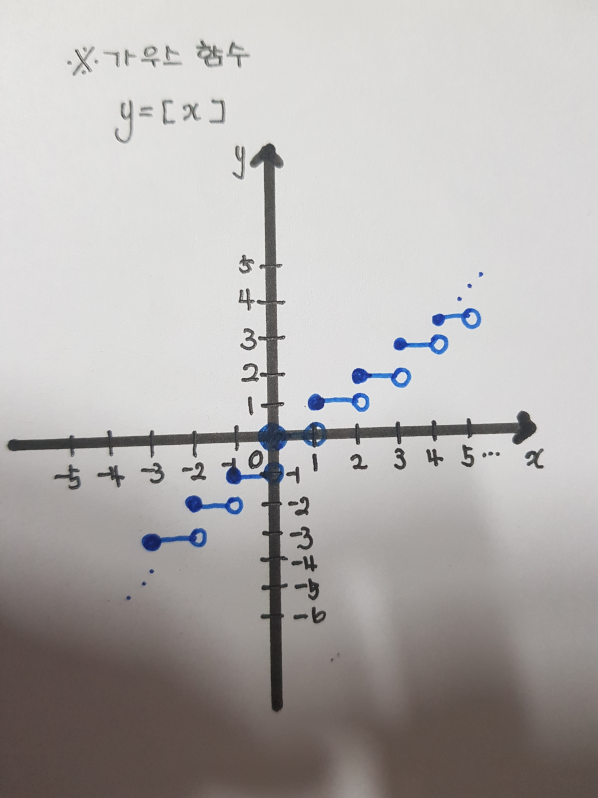
   기본적인 가우스 함수의 경우 x값의 범위를 1 단위로 나누어 계단 형태의 그래프를 얻을 수 있습니다.

다양한 형태의 가우스 함수의 응용된 그래프들

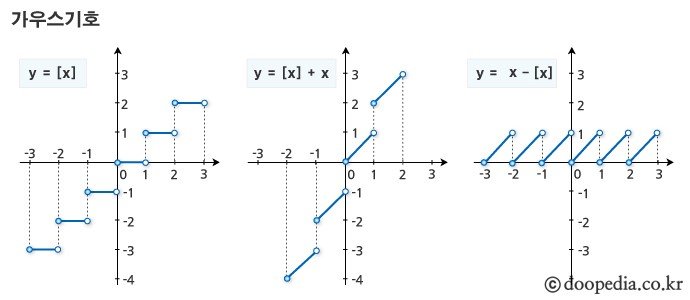
(사진출처: doopedia.co.kr)

밑에 다양한 형태의 가우스 함수의 그래프도 제가 직접 그리려고 했는데 제 방 조명이 영 아니네요 그림자도 그림에 너무 많이 잡히고 제 글씨도 엉망이여서 사진은 두산백과에서 퍼왔습니다.

어제 오늘 너무 덥네요. 건강 잘 챙기시고요. 지금까지 yurizard(주노쌤)이였습니다.
대문그림 그려주신 @marginshort 님께 감사드립니다 ^^